Krummhörn (1720-1850) selective episodes

Loading details

source("0__helpers.R")
opts_chunk$set(warning=TRUE, cache = FALSE,tidy=FALSE,dev=c('png'),fig.width=20,fig.height=12.5)

make_path = function(file) {
    get_coefficient_path(file, "krmh")
}
# options for each chunk calling knit_child
opts_chunk$set(warning=FALSE, message = FALSE, echo = FALSE)

Analysis description

Data subset

The krmh.1 dataset contains only those participants where paternal age is known, the birthdate is between 1720 and 1850 and the marriage is known (meaning we know when it started and how it ended by spousal death). In known marriages we can assume that missing death dates for the kids mean that they migrated out.

Model description

All of the following models have the following in common:

Estimation

We fit all models using brms v. 1.2.0, a Bayesian regression analysis statistical package. brms uses Stan, a probabilistic programming langugage to fit models using Hamiltonian Monte Carlo.

Covariates

As in our main models we adjust for average paternal age in the family, birth cohort (birth years in five equally large bins), for male sex, for age at paternal and maternal loss (0-1, 2-5, 6-10, …, 41-45, 45+, unknown), for maternal age (bins of 14-20, 20-35 and 35-50), for the number of siblings, for the number of older siblings (0-5, 5+) and for being last born.

Model stratification

We added random intercepts for each family (father-mother dyad). We then controlled for the average paternal age in the family. Hence, the paternal age effects in the plot are split into those between families and those within families or between siblings. We are interested in the effect of paternal age between siblings, as this effect cannot be explained by e.g. genetic propensities of the father to reproduce late.

e1: Survival to first year

Here, we predict the probability that the anchor survives the first year of life. All children born to this father are compared, if their death date is known or their survival can be inferred (from later marriage or children).

Model summary

Full summary

model_summary = summary(model, use_cache = FALSE, priors = TRUE)
print(model_summary)

##  Family: bernoulli(cauchit) 
## Formula: survive1y ~ paternalage + birth_cohort + male + maternalage.factor + paternalage.mean + paternal_loss + maternal_loss + older_siblings + nr.siblings + last_born + (1 | idParents) 
##    Data: model_data (Number of observations: 9447) 
## Samples: 6 chains, each with iter = 1000; warmup = 500; thin = 1; 
##          total post-warmup samples = 3000
##    WAIC: Not computed
##  
## Priors: 
## b ~ normal(0,5)
## sd ~ student_t(3, 0, 5)
## 
## Group-Level Effects: 
## ~idParents (Number of levels: 2186) 
##               Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sd(Intercept)     0.84      0.15     0.53      1.1        693    1
## 
## Population-Level Effects: 
##                        Estimate Est.Error l-95% CI u-95% CI Eff.Sample
## Intercept                  4.04      0.61     2.82     5.24       2046
## paternalage               -0.77      0.36    -1.46    -0.09       1442
## birth_cohort1760M1765     -0.05      0.42    -0.83     0.83       3000
## birth_cohort1765M1770     -0.18      0.39    -0.93     0.60       1758
## birth_cohort1770M1775      0.01      0.40    -0.77     0.83       1811
## birth_cohort1775M1780     -0.47      0.33    -1.11     0.17       1572
## birth_cohort1780M1785     -0.40      0.34    -1.11     0.26       1583
## birth_cohort1785M1790     -0.15      0.40    -0.90     0.68       1756
## birth_cohort1790M1795      0.54      0.44    -0.28     1.47       3000
## birth_cohort1795M1800     -0.39      0.32    -1.02     0.23       1157
## birth_cohort1800M1805      0.38      0.39    -0.37     1.18       1819
## birth_cohort1805M1810     -0.52      0.31    -1.15     0.08       1213
## birth_cohort1810M1815     -0.10      0.32    -0.74     0.52       1401
## birth_cohort1815M1820      0.70      0.40    -0.07     1.53       1878
## birth_cohort1820M1825      0.89      0.44     0.06     1.83       1943
## birth_cohort1825M1830      0.84      0.42     0.05     1.68       2091
## birth_cohort1830M1835      0.32      0.36    -0.35     1.04       1738
## male1                     -0.35      0.14    -0.62    -0.08       3000
## maternalage.factor1420     0.02      0.57    -0.95     1.28       3000
## maternalage.factor3550    -0.29      0.23    -0.73     0.16       3000
## paternalage.mean           0.91      0.38     0.17     1.64       1529
## paternal_loss01           -1.09      0.49    -1.98    -0.06       2059
## paternal_loss15           -0.90      0.35    -1.58    -0.21       1764
## paternal_loss510          -0.26      0.38    -0.98     0.50       1889
## paternal_loss1015         -0.46      0.32    -1.08     0.18       1605
## paternal_loss1520         -0.68      0.29    -1.25    -0.12       1514
## paternal_loss2025         -0.30      0.30    -0.91     0.27       1454
## paternal_loss2530         -0.31      0.29    -0.91     0.25       1579
## paternal_loss3035         -0.09      0.30    -0.66     0.50       1688
## paternal_loss3540         -0.07      0.31    -0.65     0.53       1818
## paternal_loss4045         -0.79      0.28    -1.31    -0.23       1664
## maternal_loss01           -2.53      0.30    -3.12    -1.95       2164
## maternal_loss15           -0.72      0.35    -1.38     0.00       3000
## maternal_loss510          -0.48      0.34    -1.13     0.21       3000
## maternal_loss1015         -0.27      0.34    -0.93     0.44       3000
## maternal_loss1520         -0.15      0.36    -0.80     0.61       3000
## maternal_loss2025         -0.20      0.31    -0.80     0.43       3000
## maternal_loss2530          0.12      0.32    -0.48     0.78       3000
## maternal_loss3035         -0.40      0.26    -0.89     0.12       3000
## maternal_loss3540         -0.33      0.26    -0.82     0.19       3000
## maternal_loss4045         -0.25      0.28    -0.78     0.30       3000
## older_siblings1            0.51      0.22     0.09     0.93       3000
## older_siblings2            0.81      0.26     0.31     1.34       1604
## older_siblings3            1.22      0.32     0.59     1.86       1592
## older_siblings4            1.33      0.38     0.62     2.11       1453
## older_siblings5P           2.38      0.53     1.38     3.44       1290
## nr.siblings               -0.33      0.04    -0.41    -0.25       1452
## last_born1                -0.06      0.20    -0.43     0.34       3000
##                        Rhat
## Intercept                 1
## paternalage               1
## birth_cohort1760M1765     1
## birth_cohort1765M1770     1
## birth_cohort1770M1775     1
## birth_cohort1775M1780     1
## birth_cohort1780M1785     1
## birth_cohort1785M1790     1
## birth_cohort1790M1795     1
## birth_cohort1795M1800     1
## birth_cohort1800M1805     1
## birth_cohort1805M1810     1
## birth_cohort1810M1815     1
## birth_cohort1815M1820     1
## birth_cohort1820M1825     1
## birth_cohort1825M1830     1
## birth_cohort1830M1835     1
## male1                     1
## maternalage.factor1420    1
## maternalage.factor3550    1
## paternalage.mean          1
## paternal_loss01           1
## paternal_loss15           1
## paternal_loss510          1
## paternal_loss1015         1
## paternal_loss1520         1
## paternal_loss2025         1
## paternal_loss2530         1
## paternal_loss3035         1
## paternal_loss3540         1
## paternal_loss4045         1
## maternal_loss01           1
## maternal_loss15           1
## maternal_loss510          1
## maternal_loss1015         1
## maternal_loss1520         1
## maternal_loss2025         1
## maternal_loss2530         1
## maternal_loss3035         1
## maternal_loss3540         1
## maternal_loss4045         1
## older_siblings1           1
## older_siblings2           1
## older_siblings3           1
## older_siblings4           1
## older_siblings5P          1
## nr.siblings               1
## last_born1                1
## 
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
## is a crude measure of effective sample size, and Rhat is the potential 
## scale reduction factor on split chains (at convergence, Rhat = 1).

Table of fixed effects

Estimates are exp(b). When they are referring to the hurdle (hu) component, or a dichotomous outcome, they are odds ratios, when they are referring to a Poisson component, they are hazard ratios. In both cases, they are presented with 95% credibility intervals. To see the effects on the response scale (probability or number of children), consult the marginal effect plots.

fixed_eff = data.frame(model_summary$fixed, check.names = F)
fixed_eff$Est.Error = fixed_eff$Eff.Sample = fixed_eff$Rhat = NULL
fixed_eff$`Odds/hazard ratio` = exp(fixed_eff$Estimate)
fixed_eff$`OR/HR low 95%` = exp(fixed_eff$`l-95% CI`)
fixed_eff$`OR/HR high 95%` = exp(fixed_eff$`u-95% CI`)
fixed_eff = fixed_eff %>% select(`Odds/hazard ratio`, `OR/HR low 95%`, `OR/HR high 95%`)
pander::pander(fixed_eff)

	Odds/hazard ratio	OR/HR low 95%	OR/HR high 95%
Intercept	56.94	16.78	189.1
paternalage	0.4628	0.2319	0.9183
birth_cohort1760M1765	0.9553	0.4366	2.293
birth_cohort1765M1770	0.8391	0.3939	1.818
birth_cohort1770M1775	1.015	0.4647	2.285
birth_cohort1775M1780	0.6254	0.3304	1.185
birth_cohort1780M1785	0.6685	0.3296	1.299
birth_cohort1785M1790	0.8577	0.4058	1.978
birth_cohort1790M1795	1.722	0.7521	4.36
birth_cohort1795M1800	0.6786	0.3619	1.261
birth_cohort1800M1805	1.464	0.6884	3.26
birth_cohort1805M1810	0.5973	0.3155	1.084
birth_cohort1810M1815	0.9019	0.4794	1.683
birth_cohort1815M1820	2.014	0.9279	4.599
birth_cohort1820M1825	2.424	1.057	6.228
birth_cohort1825M1830	2.321	1.053	5.387
birth_cohort1830M1835	1.381	0.7046	2.826
male1	0.7073	0.5358	0.9222
maternalage.factor1420	1.015	0.3877	3.59
maternalage.factor3550	0.7505	0.4821	1.172
paternalage.mean	2.496	1.19	5.138
paternal_loss01	0.3362	0.1387	0.9442
paternal_loss15	0.4071	0.207	0.8089
paternal_loss510	0.7727	0.3737	1.652
paternal_loss1015	0.6311	0.3394	1.193
paternal_loss1520	0.5071	0.2858	0.8892
paternal_loss2025	0.7391	0.4044	1.315
paternal_loss2530	0.7316	0.4005	1.286
paternal_loss3035	0.9139	0.5182	1.652
paternal_loss3540	0.9337	0.5228	1.705
paternal_loss4045	0.4558	0.271	0.7942
maternal_loss01	0.08004	0.04402	0.1428
maternal_loss15	0.4863	0.2513	0.9986
maternal_loss510	0.6159	0.3236	1.234
maternal_loss1015	0.7606	0.3937	1.552
maternal_loss1520	0.8636	0.449	1.837
maternal_loss2025	0.8158	0.4513	1.538
maternal_loss2530	1.124	0.6173	2.188
maternal_loss3035	0.6707	0.4112	1.131
maternal_loss3540	0.7223	0.4402	1.211
maternal_loss4045	0.7813	0.4602	1.348
older_siblings1	1.657	1.095	2.525
older_siblings2	2.257	1.362	3.821
older_siblings3	3.371	1.806	6.429
older_siblings4	3.792	1.865	8.223
older_siblings5P	10.79	3.96	31.27
nr.siblings	0.7186	0.6614	0.7811
last_born1	0.9385	0.6482	1.404

Paternal age effect

pander::pander(paternal_age_10y_effect(model))

effect	median_estimate	ci_95	ci_80
estimate father 25y	0.91	[0.89;0.93]	[0.9;0.92]
estimate father 35y	0.89	[0.85;0.92]	[0.87;0.91]
percentage change	-2.15	[-5.35;-0.21]	[-4.03;-0.82]
OR/IRR	0.46	[0.23;0.92]	[0.29;0.74]

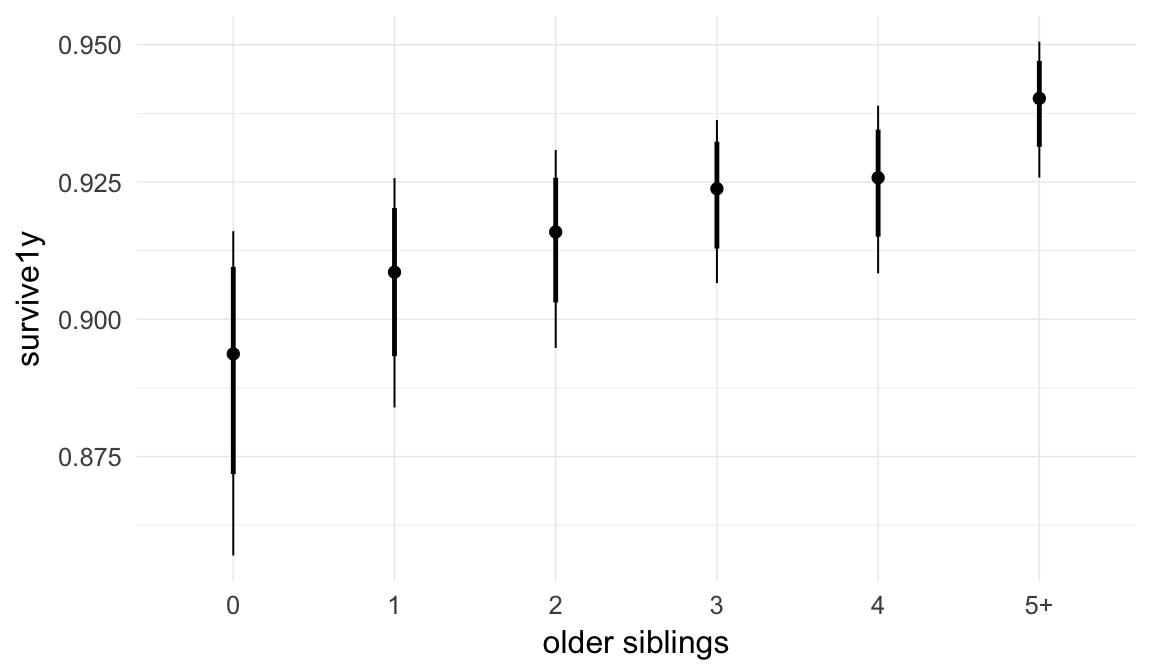
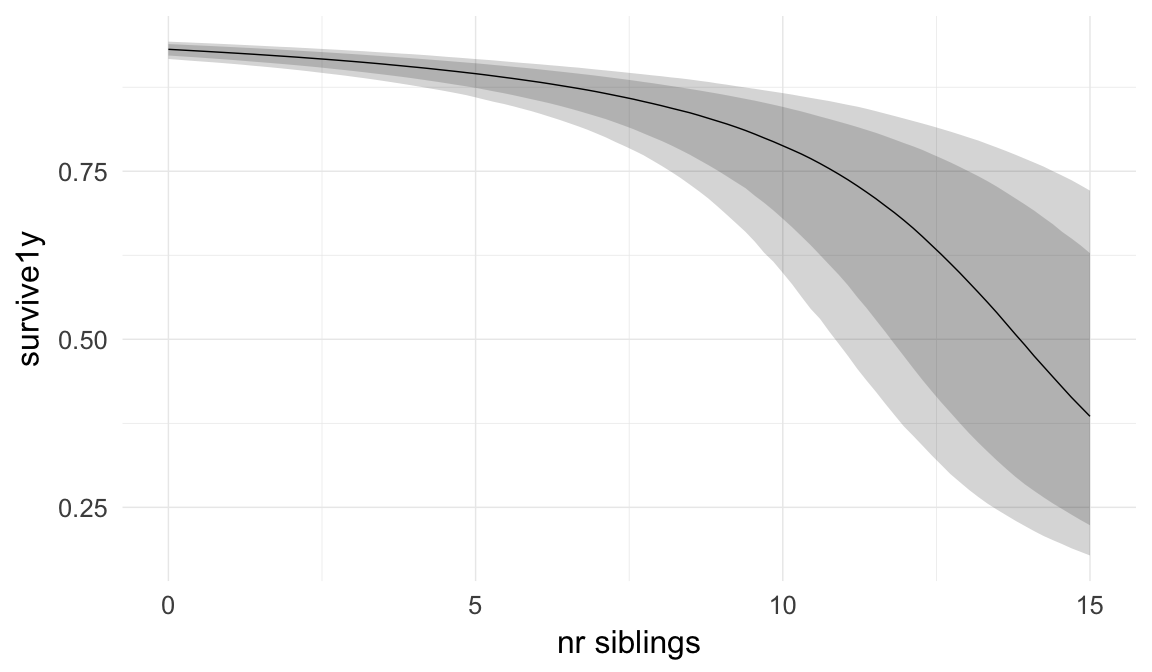
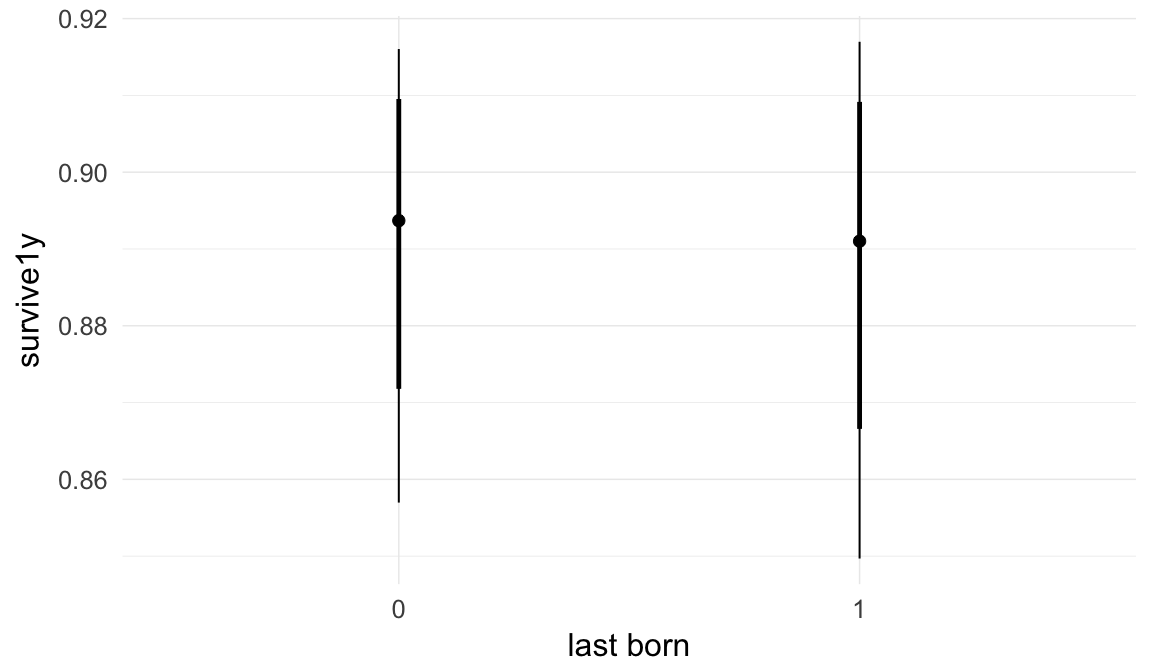
Marginal effect plots

In these marginal effect plots, we set all predictors except the one shown on the X axis to their mean and in the case of factors to their reference level. We then plot the estimated association between the X axis predictor and the outcome on the response scale (e.g. probability of survival/marriage or number of children).

plot.brmsMarginalEffects_shades(
    x = marginal_effects(model, re_formula = NA, probs = c(0.025,0.975)),
    y = marginal_effects(model, re_formula = NA, probs = c(0.1,0.9)), 
    ask = FALSE)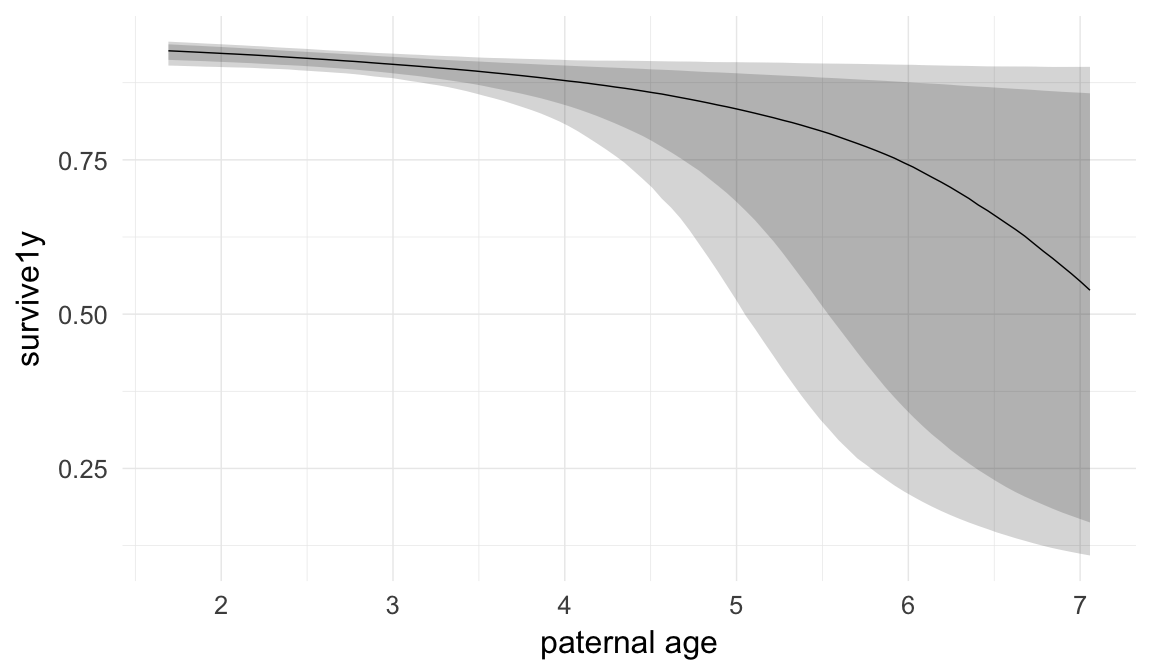

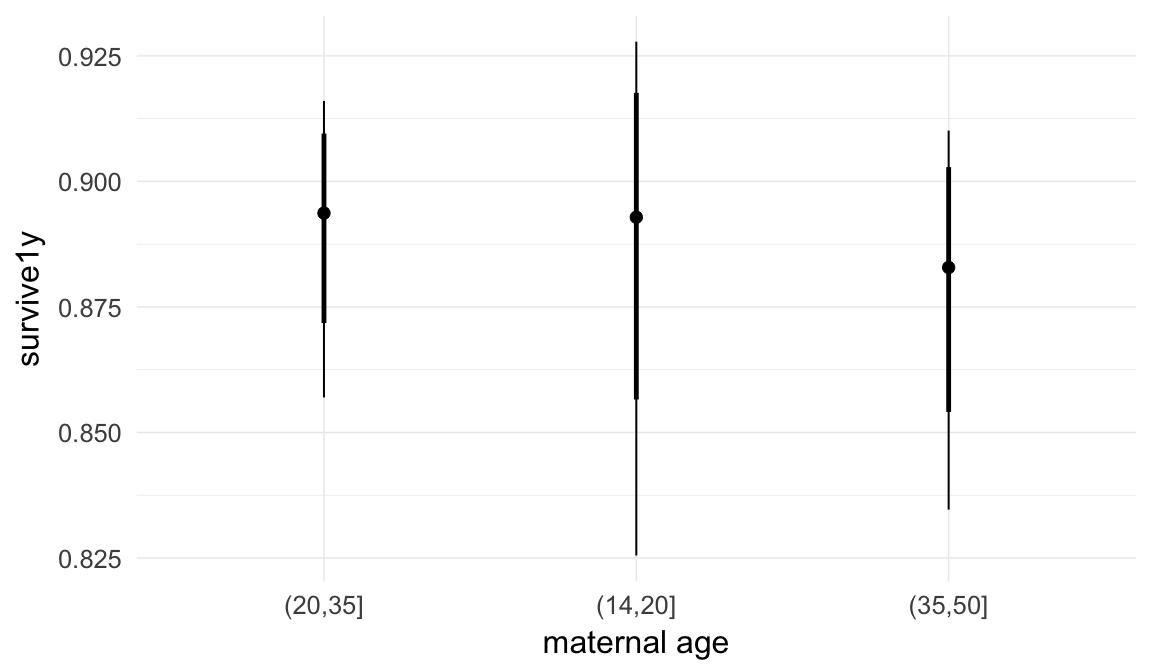
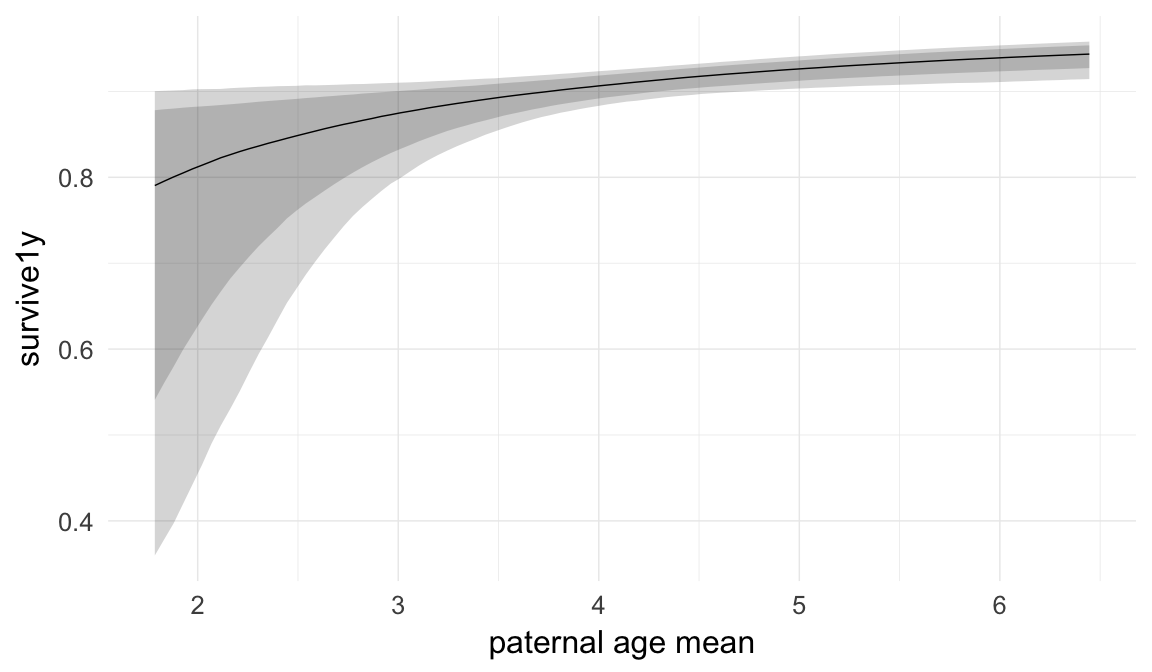
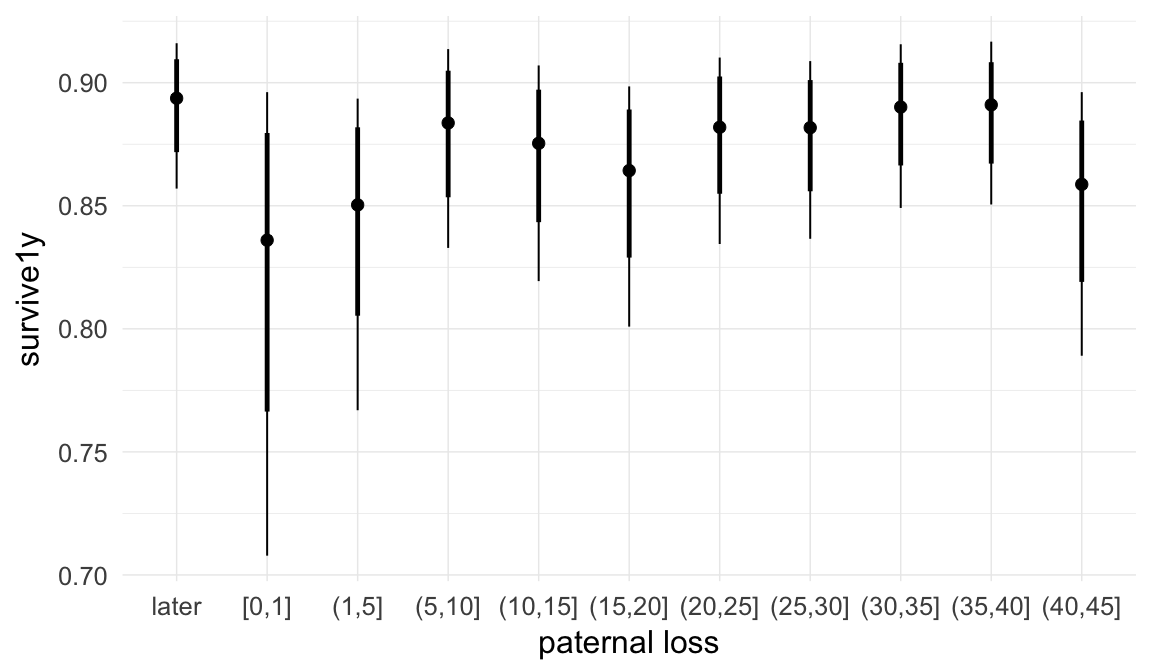
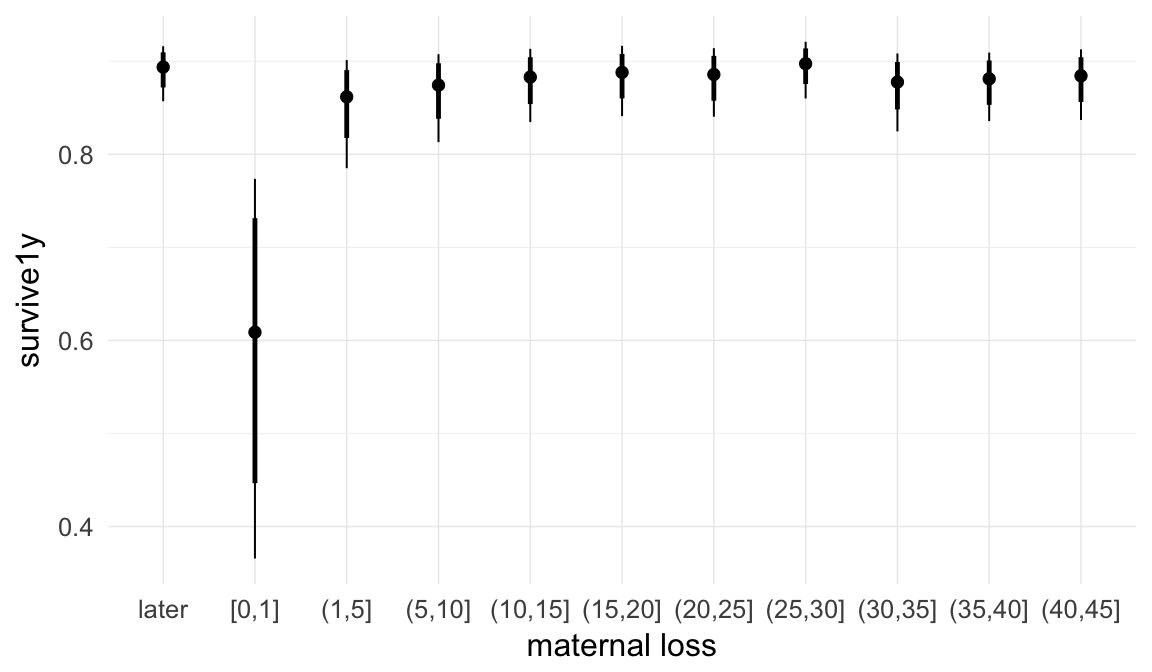
Coefficient plot

Here, we plotted the 95% posterior densities for the unexponentiated model coefficients (b_). The darkly shaded area represents the 50% credibility interval, the dark line represent the posterior mean estimate.

mcmc_areas(as.matrix(model$fit), regex_pars = "b_[^I]", point_est = "mean", prob = 0.50, prob_outer = 0.95) + ggtitle("Posterior densities with means and 50% intervals") + analysis_theme + theme(axis.text = element_text(size = 12), panel.grid = element_blank()) + xlab("Coefficient size")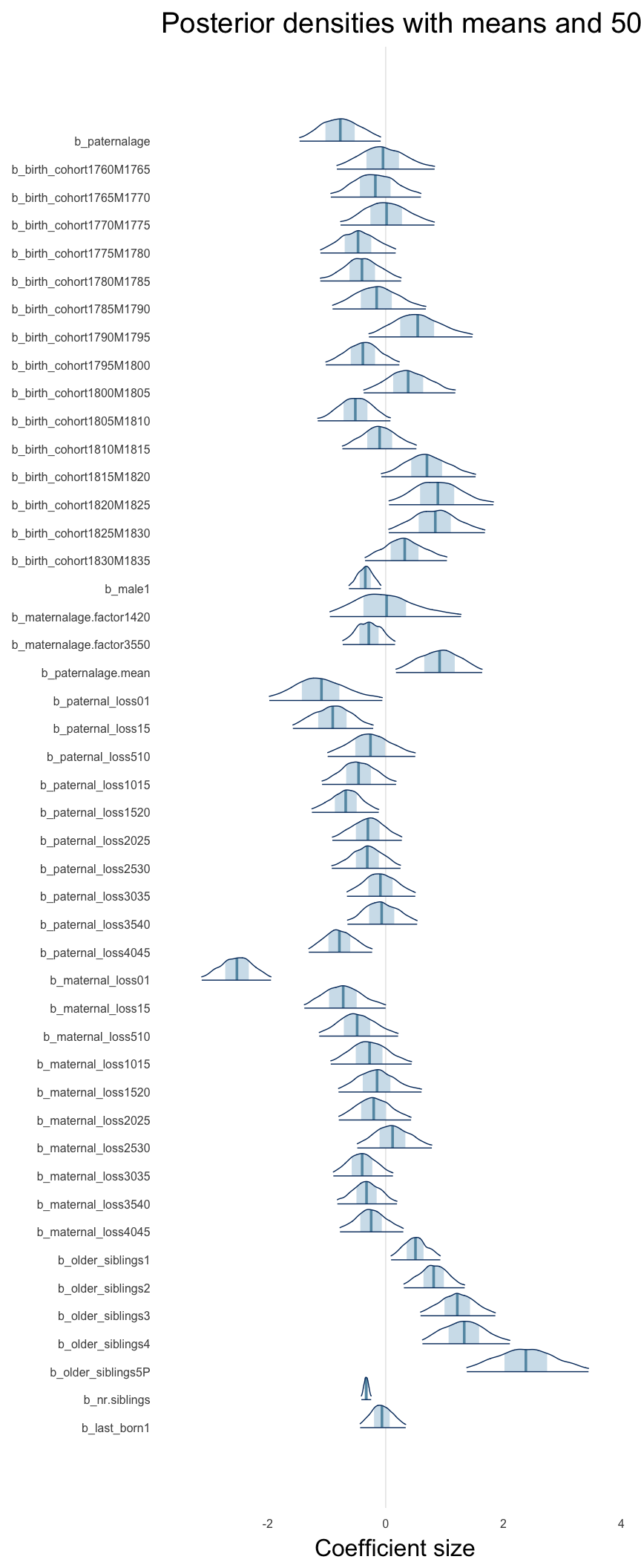

Diagnostics

These plots were made to diagnose misfit and nonconvergence.

Posterior predictive checks

In posterior predictive checks, we test whether we can approximately reproduce the real data distribution from our model.

brms::pp_check(model, re_formula = NA, type = "dens_overlay")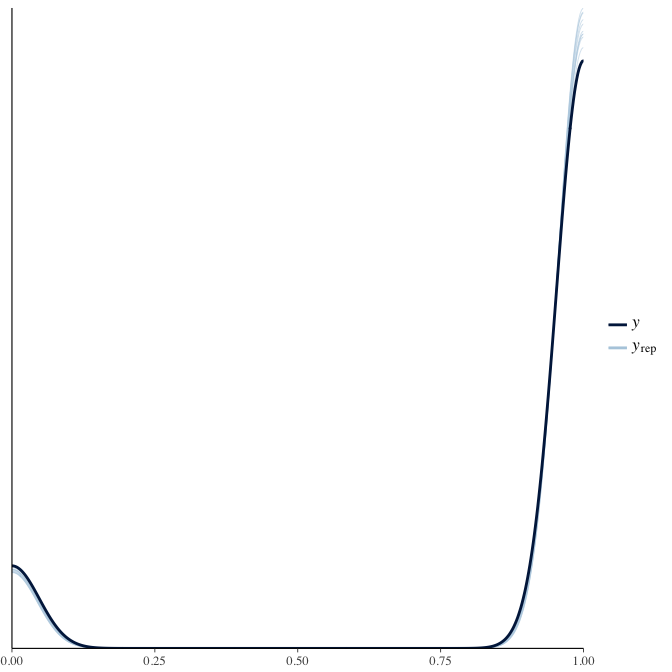

brms::pp_check(model, re_formula = NA, type = "hist")

Rhat

Did the 6 chains converge?

stanplot(model, pars = "^b_[^I]", type = 'rhat')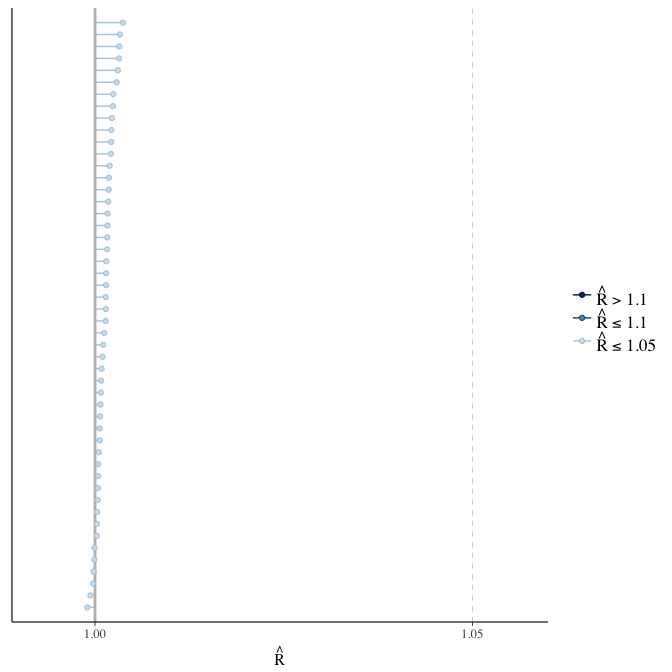

Effective sample size over average sample size

stanplot(model, pars = "^b", type = 'neff_hist')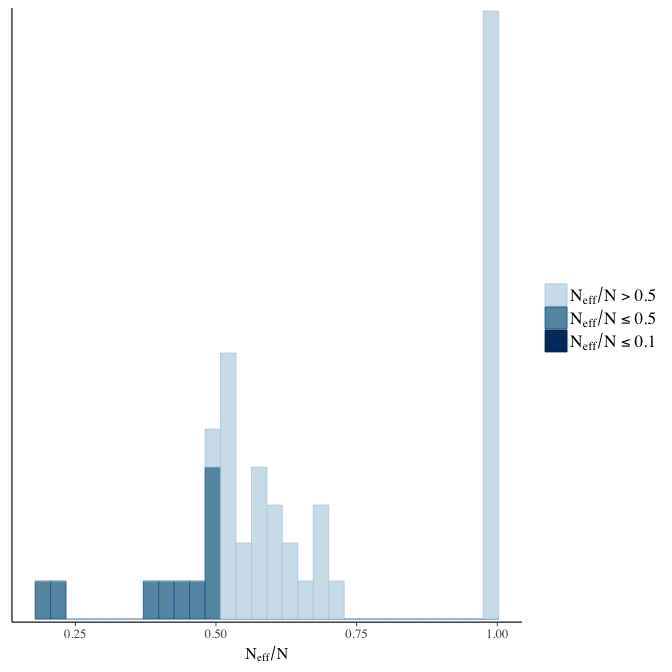

Trace plots

Trace plots are only shown in the case of nonconvergence.

if(any( summary(model)$fixed[,"Rhat"] > 1.1)) { # only do traceplots if not converged
    plot(model, N = 3, ask = FALSE)
}

File/cluster script name

This model was stored in the file: coefs/krmh/e1_survive1y.rds.

Click the following link to see the script used to generate this model:

opts_chunk$set(echo = FALSE)
clusterscript = str_replace(basename(model_filename), "\\.rds",".html")
cat("[Cluster script](" , clusterscript, ")", sep = "")

Cluster script

e2: Probability of surviving the first 15 years of life

Here, we predict the probability that the anchor survives the first fifteen of life. All children born to this father who lived at least one year are compared, if their death date is known or their survival can be inferred (from later marriage or children).

Model summary

Full summary

model_summary = summary(model, use_cache = FALSE, priors = TRUE)
print(model_summary)

##  Family: bernoulli(cauchit) 
## Formula: surviveR ~ paternalage + birth_cohort + male + maternalage.factor + paternalage.mean + paternal_loss + maternal_loss + older_siblings + nr.siblings + last_born + (1 | idParents) 
##    Data: model_data (Number of observations: 8283) 
## Samples: 6 chains, each with iter = 1000; warmup = 500; thin = 1; 
##          total post-warmup samples = 3000
##    WAIC: Not computed
##  
## Priors: 
## b ~ normal(0,5)
## sd ~ student_t(3, 0, 5)
## 
## Group-Level Effects: 
## ~idParents (Number of levels: 2149) 
##               Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sd(Intercept)     0.78      0.11     0.56     0.99        645    1
## 
## Population-Level Effects: 
##                        Estimate Est.Error l-95% CI u-95% CI Eff.Sample
## Intercept                  2.91      0.47     1.98     3.84       1911
## paternalage                0.03      0.29    -0.51     0.62       1091
## birth_cohort1760M1765      0.19      0.32    -0.39     0.84       3000
## birth_cohort1765M1770      0.15      0.29    -0.41     0.75       3000
## birth_cohort1770M1775      0.22      0.29    -0.32     0.83       2208
## birth_cohort1775M1780     -0.28      0.25    -0.76     0.20       1779
## birth_cohort1780M1785     -0.32      0.24    -0.79     0.16       1707
## birth_cohort1785M1790      0.57      0.34    -0.04     1.28       3000
## birth_cohort1790M1795     -0.07      0.24    -0.53     0.38       1603
## birth_cohort1795M1800      0.71      0.30     0.14     1.32       3000
## birth_cohort1800M1805      0.26      0.24    -0.20     0.76       1631
## birth_cohort1805M1810     -0.02      0.23    -0.46     0.42       1229
## birth_cohort1810M1815      0.96      0.31     0.38     1.59       3000
## birth_cohort1815M1820      1.30      0.33     0.69     1.96       3000
## birth_cohort1820M1825      0.34      0.24    -0.11     0.81       1648
## birth_cohort1825M1830      0.65      0.26     0.14     1.18       2053
## birth_cohort1830M1835      1.16      0.34     0.55     1.88       3000
## male1                     -0.09      0.10    -0.28     0.10       3000
## maternalage.factor1420    -0.75      0.41    -1.49     0.15       3000
## maternalage.factor3550    -0.23      0.16    -0.54     0.09       3000
## paternalage.mean           0.00      0.30    -0.61     0.55       1147
## paternal_loss01           -0.72      0.36    -1.41     0.02       3000
## paternal_loss15           -0.56      0.27    -1.09    -0.04       1770
## paternal_loss510           0.12      0.28    -0.41     0.67       2161
## paternal_loss1015         -0.38      0.23    -0.84     0.06       1714
## paternal_loss1520         -0.15      0.23    -0.61     0.28       1753
## paternal_loss2025         -0.28      0.22    -0.71     0.15       1598
## paternal_loss2530          0.06      0.23    -0.38     0.52       1726
## paternal_loss3035         -0.11      0.21    -0.53     0.30       1663
## paternal_loss3540          0.18      0.23    -0.28     0.65       1923
## paternal_loss4045         -0.13      0.24    -0.59     0.35       2143
## maternal_loss01           -1.27      0.31    -1.88    -0.65       3000
## maternal_loss15           -0.85      0.24    -1.32    -0.37       1809
## maternal_loss510          -0.52      0.23    -0.96    -0.06       2028
## maternal_loss1015         -0.60      0.22    -1.02    -0.16       2144
## maternal_loss1520         -0.58      0.23    -1.01    -0.13       3000
## maternal_loss2025         -0.46      0.23    -0.89     0.00       1975
## maternal_loss2530         -0.24      0.22    -0.66     0.19       3000
## maternal_loss3035         -0.13      0.22    -0.56     0.32       3000
## maternal_loss3540         -0.18      0.19    -0.55     0.21       3000
## maternal_loss4045         -0.35      0.20    -0.72     0.04       3000
## older_siblings1           -0.28      0.18    -0.63     0.08       3000
## older_siblings2           -0.20      0.22    -0.63     0.21       1380
## older_siblings3           -0.32      0.26    -0.86     0.17       1242
## older_siblings4           -0.25      0.32    -0.90     0.34       1164
## older_siblings5P           0.25      0.43    -0.59     1.08       1069
## nr.siblings               -0.11      0.04    -0.18    -0.04       1298
## last_born1                -0.04      0.14    -0.32     0.24       3000
##                        Rhat
## Intercept              1.00
## paternalage            1.00
## birth_cohort1760M1765  1.00
## birth_cohort1765M1770  1.00
## birth_cohort1770M1775  1.00
## birth_cohort1775M1780  1.00
## birth_cohort1780M1785  1.00
## birth_cohort1785M1790  1.00
## birth_cohort1790M1795  1.00
## birth_cohort1795M1800  1.00
## birth_cohort1800M1805  1.01
## birth_cohort1805M1810  1.01
## birth_cohort1810M1815  1.00
## birth_cohort1815M1820  1.00
## birth_cohort1820M1825  1.00
## birth_cohort1825M1830  1.00
## birth_cohort1830M1835  1.00
## male1                  1.00
## maternalage.factor1420 1.00
## maternalage.factor3550 1.00
## paternalage.mean       1.00
## paternal_loss01        1.00
## paternal_loss15        1.00
## paternal_loss510       1.00
## paternal_loss1015      1.00
## paternal_loss1520      1.00
## paternal_loss2025      1.00
## paternal_loss2530      1.00
## paternal_loss3035      1.00
## paternal_loss3540      1.00
## paternal_loss4045      1.00
## maternal_loss01        1.00
## maternal_loss15        1.00
## maternal_loss510       1.00
## maternal_loss1015      1.00
## maternal_loss1520      1.00
## maternal_loss2025      1.00
## maternal_loss2530      1.00
## maternal_loss3035      1.00
## maternal_loss3540      1.00
## maternal_loss4045      1.00
## older_siblings1        1.00
## older_siblings2        1.00
## older_siblings3        1.00
## older_siblings4        1.00
## older_siblings5P       1.00
## nr.siblings            1.00
## last_born1             1.00
## 
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
## is a crude measure of effective sample size, and Rhat is the potential 
## scale reduction factor on split chains (at convergence, Rhat = 1).

Table of fixed effects

fixed_eff = data.frame(model_summary$fixed, check.names = F)
fixed_eff$Est.Error = fixed_eff$Eff.Sample = fixed_eff$Rhat = NULL
fixed_eff$`Odds/hazard ratio` = exp(fixed_eff$Estimate)
fixed_eff$`OR/HR low 95%` = exp(fixed_eff$`l-95% CI`)
fixed_eff$`OR/HR high 95%` = exp(fixed_eff$`u-95% CI`)
fixed_eff = fixed_eff %>% select(`Odds/hazard ratio`, `OR/HR low 95%`, `OR/HR high 95%`)
pander::pander(fixed_eff)

	Odds/hazard ratio	OR/HR low 95%	OR/HR high 95%
Intercept	18.29	7.21	46.5
paternalage	1.025	0.5996	1.858
birth_cohort1760M1765	1.214	0.6785	2.323
birth_cohort1765M1770	1.16	0.6653	2.116
birth_cohort1770M1775	1.25	0.7295	2.304
birth_cohort1775M1780	0.7543	0.4657	1.22
birth_cohort1780M1785	0.7264	0.4532	1.173
birth_cohort1785M1790	1.772	0.9622	3.591
birth_cohort1790M1795	0.9339	0.5903	1.468
birth_cohort1795M1800	2.034	1.151	3.757
birth_cohort1800M1805	1.297	0.8209	2.145
birth_cohort1805M1810	0.9824	0.6321	1.522
birth_cohort1810M1815	2.624	1.457	4.907
birth_cohort1815M1820	3.685	1.986	7.101
birth_cohort1820M1825	1.412	0.8962	2.252
birth_cohort1825M1830	1.925	1.15	3.271
birth_cohort1830M1835	3.188	1.73	6.526
male1	0.9123	0.7523	1.107
maternalage.factor1420	0.471	0.2264	1.157
maternalage.factor3550	0.7967	0.5827	1.092
paternalage.mean	1.004	0.5438	1.735
paternal_loss01	0.4845	0.245	1.016
paternal_loss15	0.5687	0.337	0.9656
paternal_loss510	1.126	0.6655	1.946
paternal_loss1015	0.6813	0.4339	1.059
paternal_loss1520	0.8575	0.542	1.327
paternal_loss2025	0.7555	0.4935	1.157
paternal_loss2530	1.059	0.6867	1.685
paternal_loss3035	0.8917	0.5882	1.345
paternal_loss3540	1.194	0.7575	1.913
paternal_loss4045	0.8776	0.5528	1.413
maternal_loss01	0.2806	0.1533	0.5246
maternal_loss15	0.4276	0.2674	0.6909
maternal_loss510	0.596	0.3816	0.9434
maternal_loss1015	0.5468	0.3591	0.8502
maternal_loss1520	0.5596	0.3639	0.8782
maternal_loss2025	0.6312	0.4116	0.9968
maternal_loss2530	0.7829	0.5191	1.205
maternal_loss3035	0.8788	0.5728	1.381
maternal_loss3540	0.8336	0.5773	1.228
maternal_loss4045	0.7029	0.4864	1.042
older_siblings1	0.7576	0.5325	1.089
older_siblings2	0.8172	0.5314	1.234
older_siblings3	0.7235	0.4248	1.181
older_siblings4	0.7761	0.408	1.4
older_siblings5P	1.287	0.5562	2.938
nr.siblings	0.8972	0.8336	0.9633
last_born1	0.9609	0.7298	1.274

Paternal age effect

pander::pander(paternal_age_10y_effect(model))

effect	median_estimate	ci_95	ci_80
estimate father 25y	0.88	[0.85;0.9]	[0.86;0.89]
estimate father 35y	0.88	[0.84;0.9]	[0.85;0.9]
percentage change	0.06	[-2.69;2.73]	[-1.73;1.75]
OR/IRR	1.01	[0.6;1.86]	[0.71;1.5]

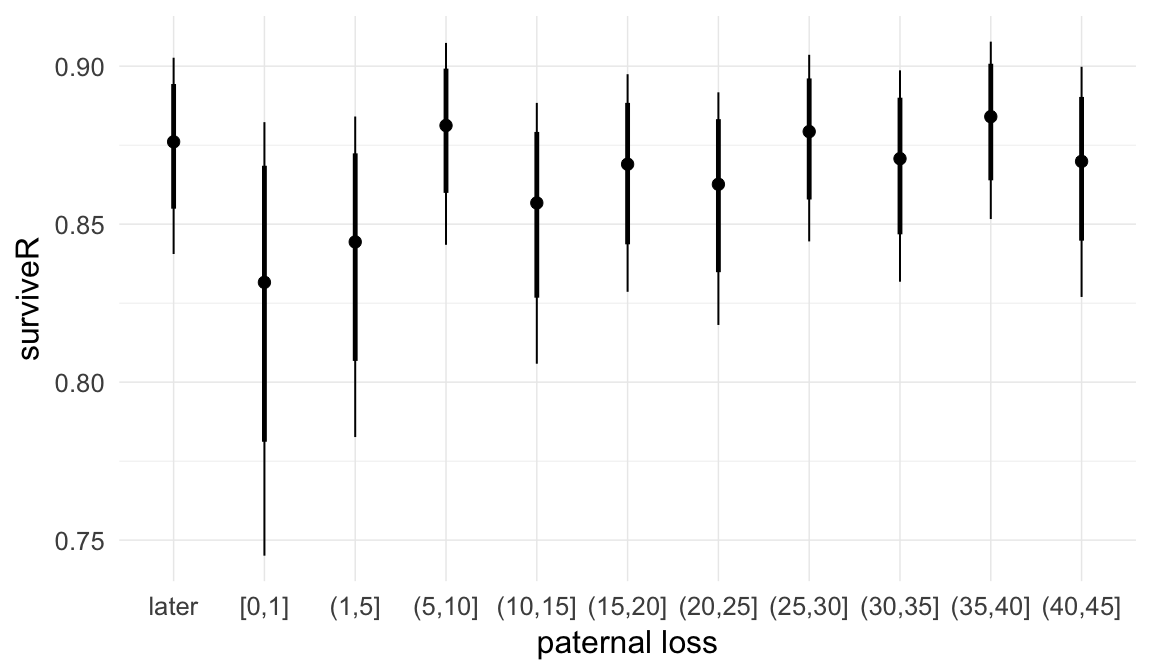
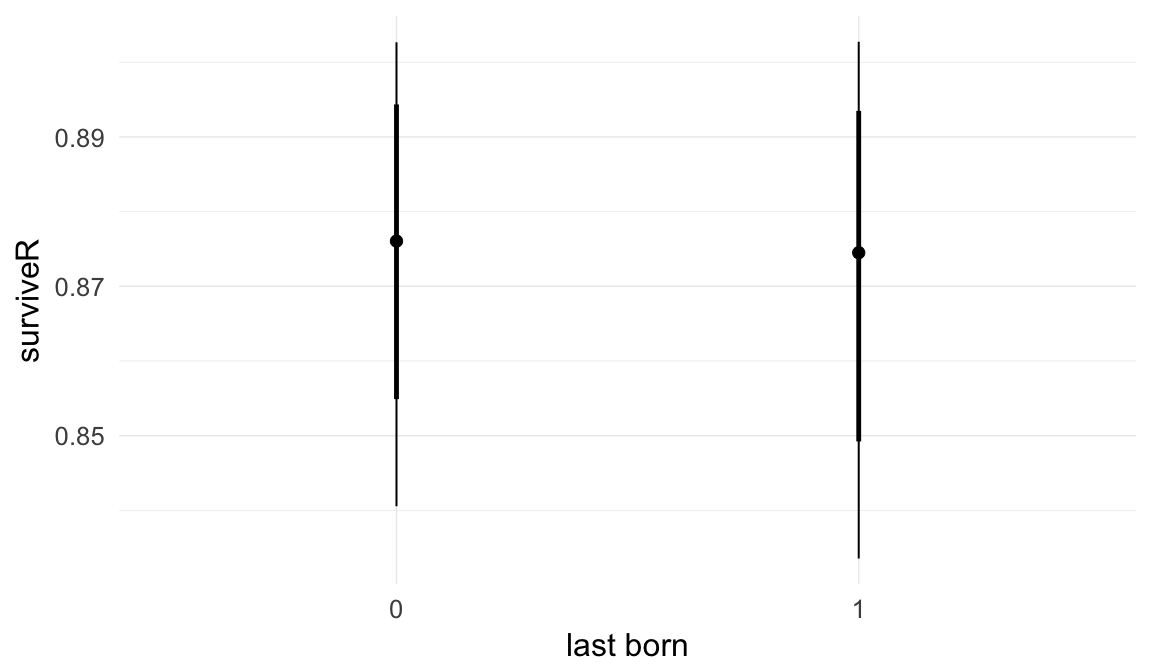
Marginal effect plots

plot.brmsMarginalEffects_shades(
    x = marginal_effects(model, re_formula = NA, probs = c(0.025,0.975)),
    y = marginal_effects(model, re_formula = NA, probs = c(0.1,0.9)), 
    ask = FALSE)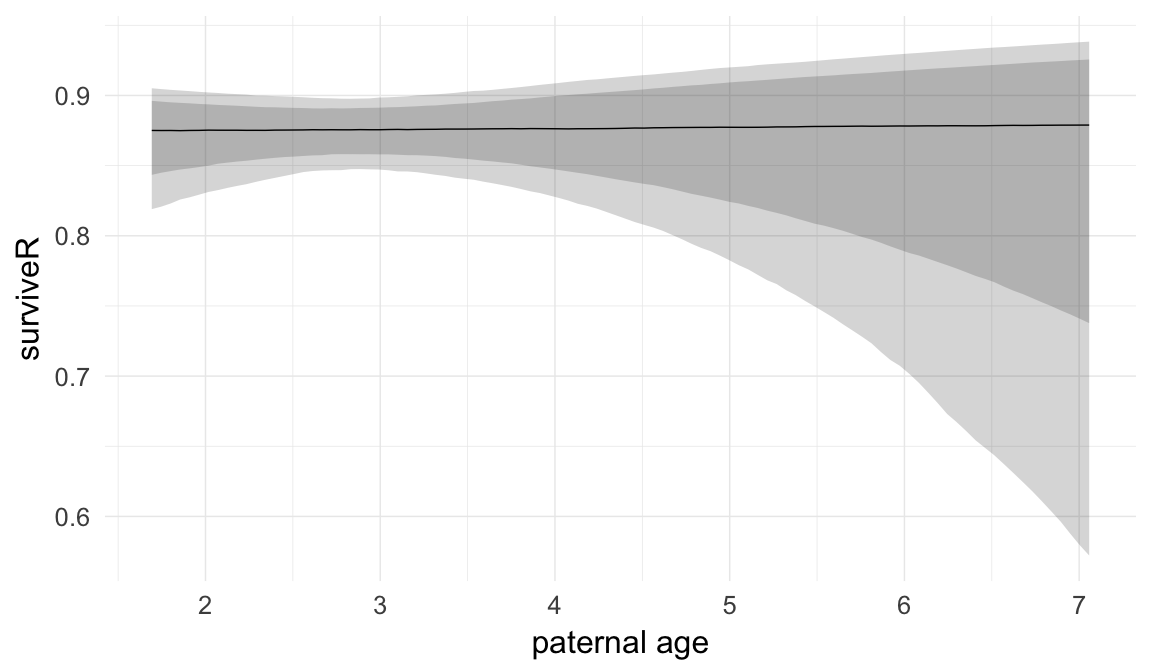

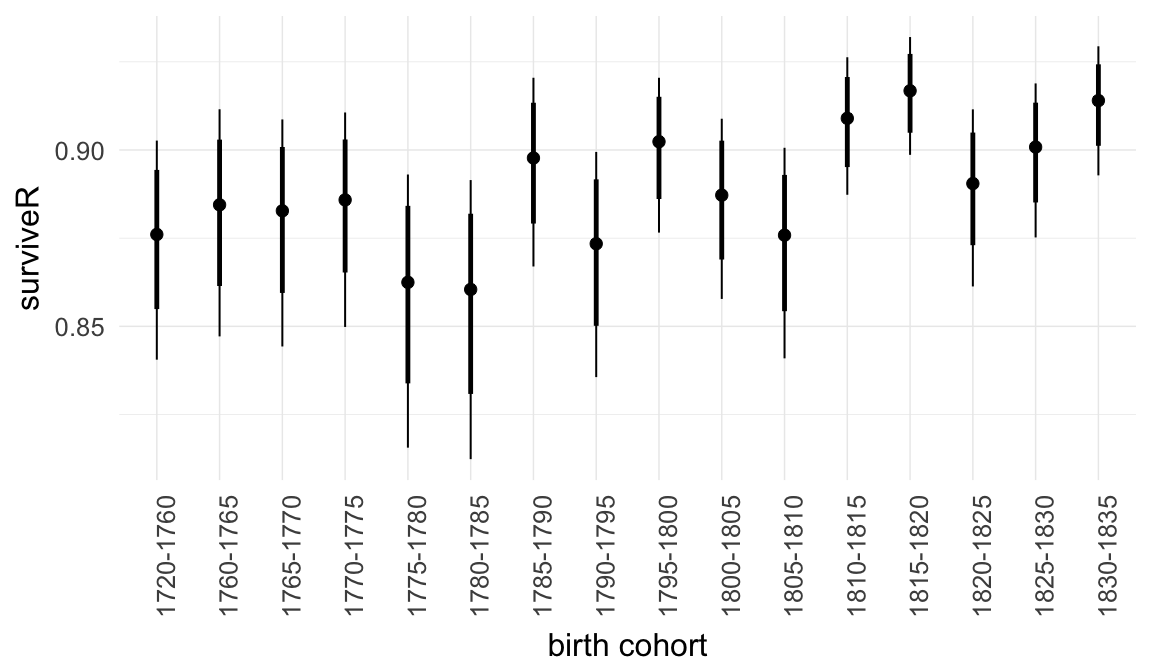
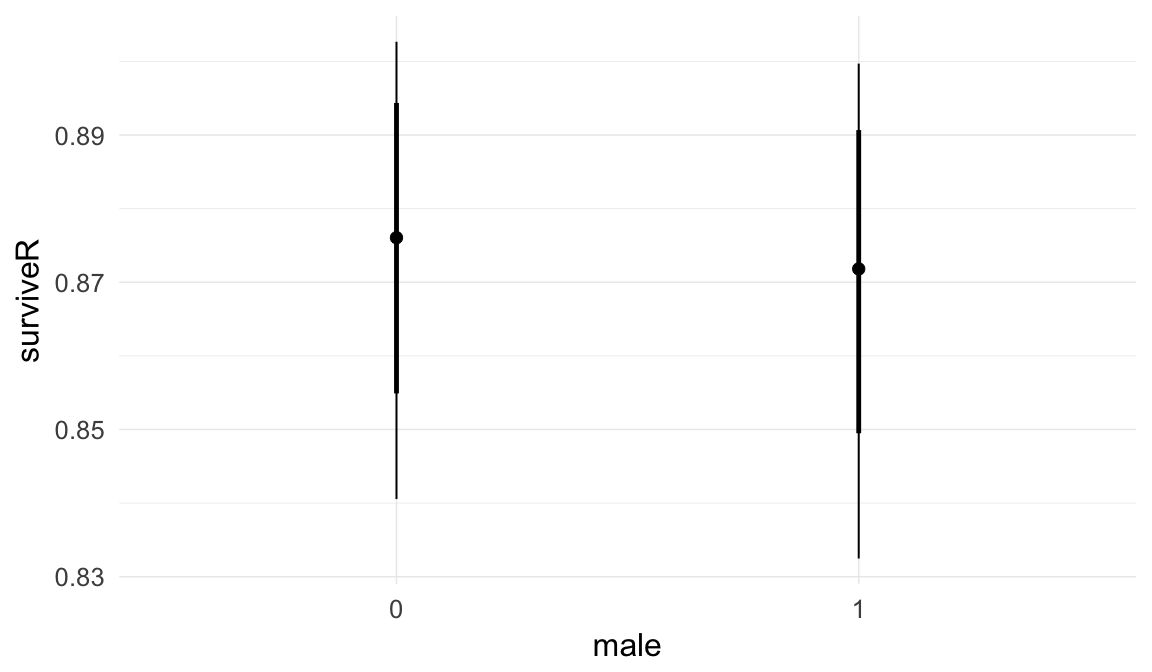
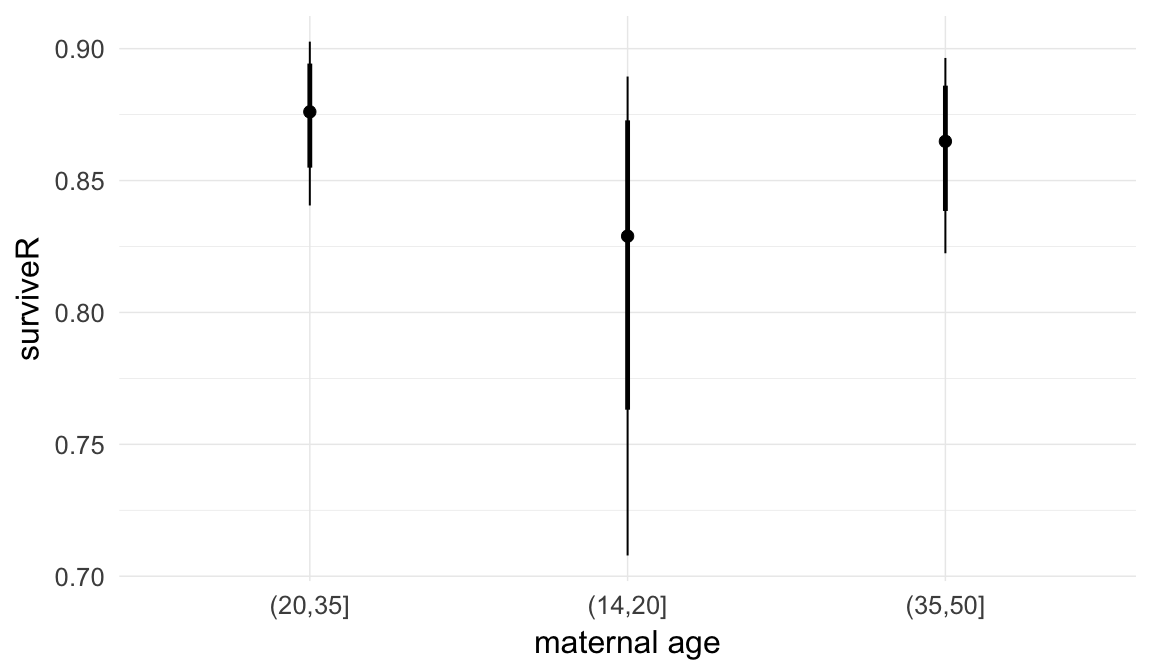
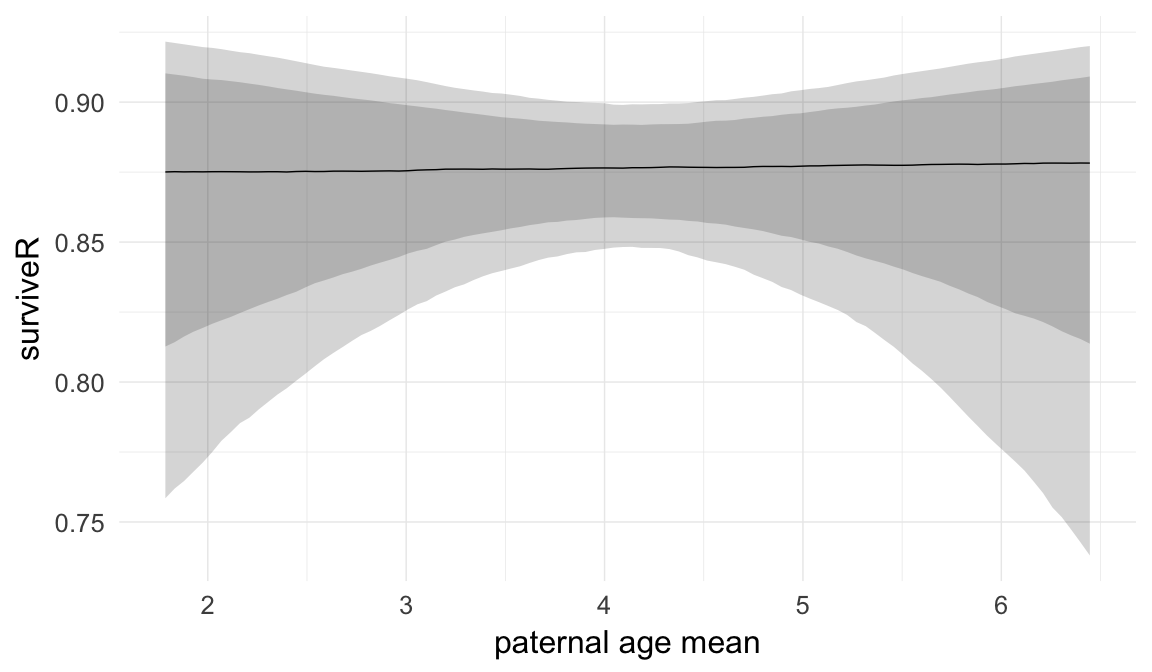
Coefficient plot

mcmc_areas(as.matrix(model$fit), regex_pars = "b_[^I]", point_est = "mean", prob = 0.50, prob_outer = 0.95) + ggtitle("Posterior densities with means and 50% intervals") + analysis_theme + theme(axis.text = element_text(size = 12), panel.grid = element_blank()) + xlab("Coefficient size")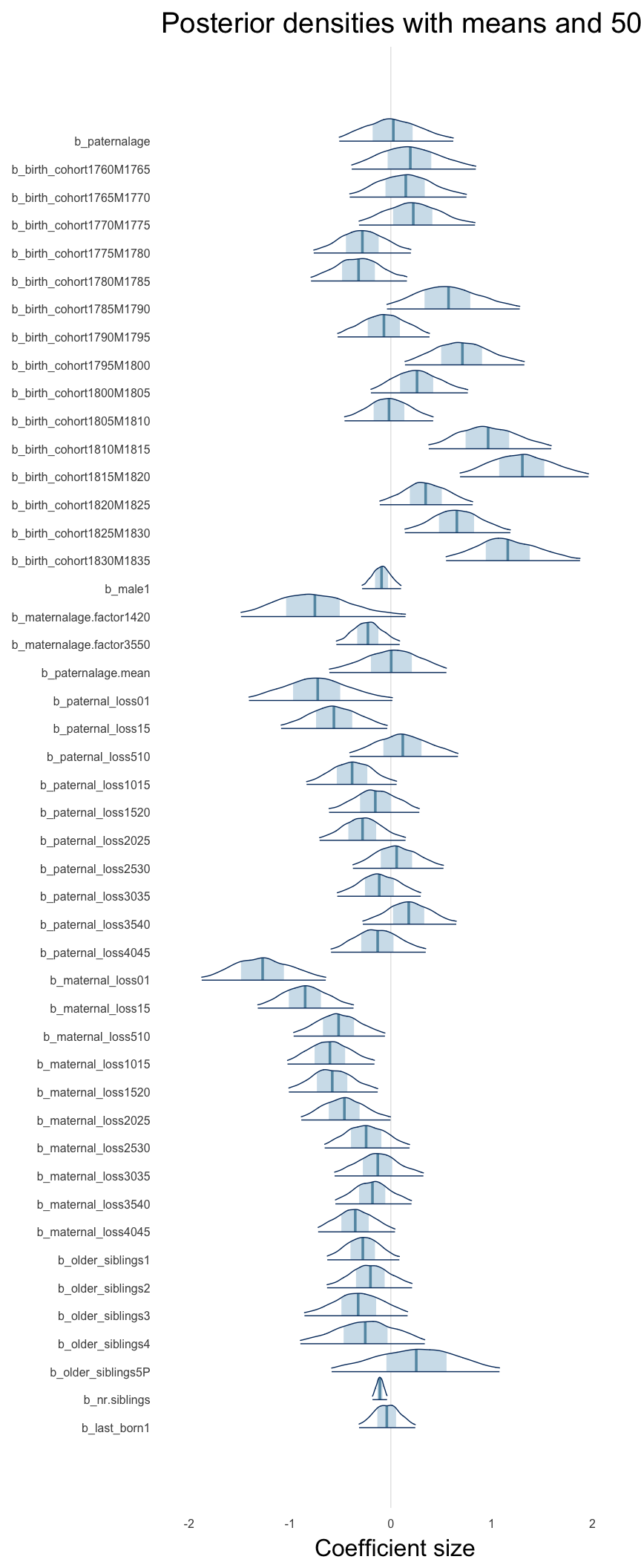

Diagnostics

These plots were made to diagnose misfit and nonconvergence.

Posterior predictive checks

In posterior predictive checks, we test whether we can approximately reproduce the real data distribution from our model.

brms::pp_check(model, re_formula = NA, type = "dens_overlay")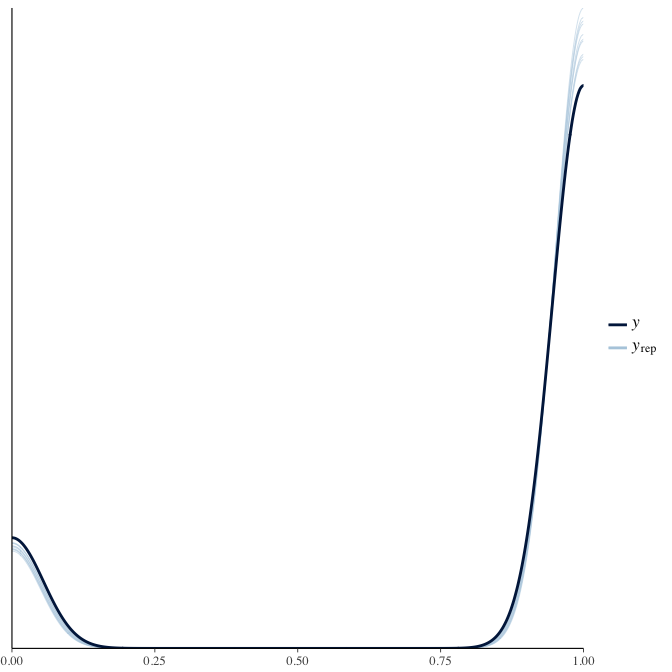

brms::pp_check(model, re_formula = NA, type = "hist")

Rhat

Did the 6 chains converge?

stanplot(model, pars = "^b_[^I]", type = 'rhat')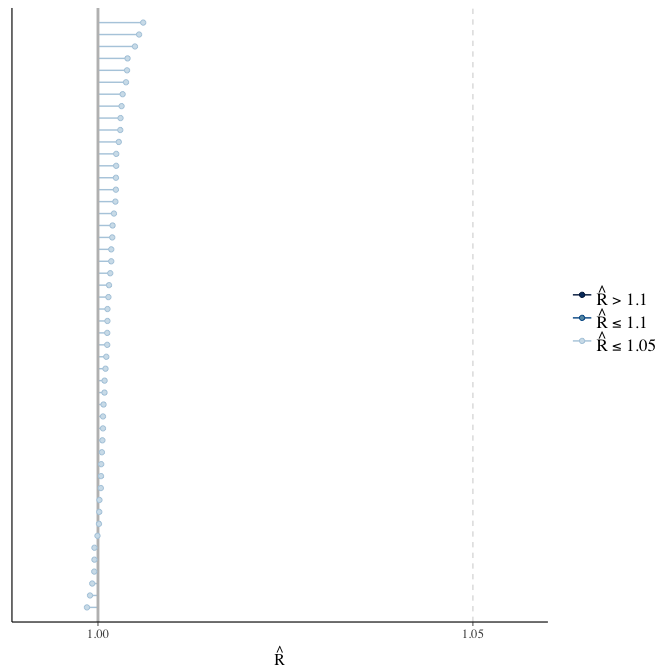

Effective sample size over average sample size

stanplot(model, pars = "^b", type = 'neff_hist')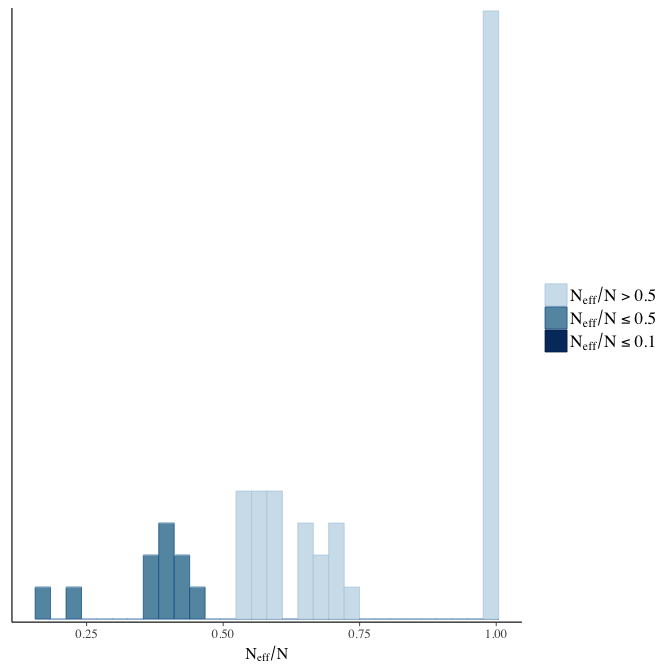

Trace plots

Trace plots are only shown in the case of nonconvergence.

if(any( summary(model)$fixed[,"Rhat"] > 1.1)) { # only do traceplots if not converged
    plot(model, N = 3, ask = FALSE)
}

File/cluster script name

This model was stored in the file: coefs/krmh/e2_surviveR.rds.

Click the following link to see the script used to generate this model:

opts_chunk$set(echo = FALSE)
clusterscript = str_replace(basename(model_filename), "\\.rds",".html")
cat("[Cluster script](" , clusterscript, ")", sep = "")

Cluster script

e3: Probability of ever marrying

Here, we predict the probability that the anchor ever marries. All anchors who reached reproductive age (15) are included.

Model summary

Full summary

model_summary = summary(model, use_cache = FALSE, priors = TRUE)
print(model_summary)

##  Family: bernoulli(cauchit) 
## Formula: ever_married ~ paternalage + birth_cohort + male + maternalage.factor + paternalage.mean + paternal_loss + maternal_loss + older_siblings + nr.siblings + last_born + (1 | idParents) 
##    Data: model_data (Number of observations: 6922) 
## Samples: 6 chains, each with iter = 1500; warmup = 1000; thin = 1; 
##          total post-warmup samples = 3000
##    WAIC: Not computed
##  
## Priors: 
## b ~ normal(0,5)
## sd ~ student_t(3, 0, 5)
## 
## Group-Level Effects: 
## ~idParents (Number of levels: 2094) 
##               Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sd(Intercept)     0.72      0.06     0.61     0.84        909    1
## 
## Population-Level Effects: 
##                        Estimate Est.Error l-95% CI u-95% CI Eff.Sample
## Intercept                  1.15      0.26     0.64     1.65       1378
## paternalage               -0.24      0.17    -0.58     0.09        878
## birth_cohort1760M1765      0.06      0.20    -0.31     0.45       1463
## birth_cohort1765M1770      0.46      0.18     0.11     0.81       1055
## birth_cohort1770M1775      0.19      0.17    -0.14     0.52        902
## birth_cohort1775M1780      0.54      0.18     0.20     0.90        908
## birth_cohort1780M1785      0.52      0.19     0.16     0.89       1051
## birth_cohort1785M1790      0.62      0.19     0.26     0.99        965
## birth_cohort1790M1795      0.46      0.17     0.12     0.79        874
## birth_cohort1795M1800      0.66      0.16     0.34     0.99        594
## birth_cohort1800M1805      0.78      0.17     0.46     1.12        617
## birth_cohort1805M1810      0.74      0.17     0.42     1.08        832
## birth_cohort1810M1815      0.70      0.16     0.39     1.03        776
## birth_cohort1815M1820      0.92      0.15     0.61     1.23        699
## birth_cohort1820M1825      0.83      0.15     0.54     1.13        639
## birth_cohort1825M1830      0.83      0.15     0.54     1.13        675
## birth_cohort1830M1835      0.87      0.16     0.58     1.19        749
## male1                     -0.50      0.06    -0.62    -0.39       3000
## maternalage.factor1420     0.38      0.39    -0.31     1.17       3000
## maternalage.factor3550     0.02      0.09    -0.16     0.20       3000
## paternalage.mean           0.11      0.18    -0.24     0.46        890
## paternal_loss01           -0.35      0.23    -0.79     0.13       3000
## paternal_loss15           -0.51      0.16    -0.81    -0.20       1570
## paternal_loss510          -0.33      0.14    -0.61    -0.05       1359
## paternal_loss1015         -0.15      0.14    -0.42     0.13       1402
## paternal_loss1520         -0.17      0.13    -0.43     0.09       1318
## paternal_loss2025         -0.23      0.13    -0.48     0.01       1308
## paternal_loss2530         -0.16      0.12    -0.40     0.08       1252
## paternal_loss3035          0.00      0.12    -0.23     0.24       1398
## paternal_loss3540         -0.15      0.12    -0.38     0.08       1379
## paternal_loss4045         -0.14      0.13    -0.40     0.13       1829
## maternal_loss01           -1.20      0.22    -1.65    -0.76       3000
## maternal_loss15           -0.40      0.15    -0.70    -0.10       3000
## maternal_loss510          -0.52      0.13    -0.78    -0.25       2020
## maternal_loss1015         -0.45      0.14    -0.71    -0.18       3000
## maternal_loss1520         -0.36      0.14    -0.63    -0.09       3000
## maternal_loss2025         -0.16      0.13    -0.42     0.11       3000
## maternal_loss2530         -0.22      0.12    -0.45     0.02       1848
## maternal_loss3035         -0.15      0.12    -0.37     0.09       1873
## maternal_loss3540          0.04      0.11    -0.17     0.25       1951
## maternal_loss4045         -0.19      0.11    -0.41     0.04       3000
## older_siblings1           -0.01      0.09    -0.18     0.19       1672
## older_siblings2            0.13      0.12    -0.11     0.37       1132
## older_siblings3            0.04      0.15    -0.25     0.34        971
## older_siblings4            0.13      0.20    -0.26     0.52        925
## older_siblings5P           0.29      0.26    -0.20     0.82        866
## nr.siblings               -0.03      0.02    -0.08     0.02       1109
## last_born1                -0.06      0.08    -0.21     0.09       3000
##                        Rhat
## Intercept              1.01
## paternalage            1.00
## birth_cohort1760M1765  1.00
## birth_cohort1765M1770  1.00
## birth_cohort1770M1775  1.00
## birth_cohort1775M1780  1.00
## birth_cohort1780M1785  1.00
## birth_cohort1785M1790  1.00
## birth_cohort1790M1795  1.00
## birth_cohort1795M1800  1.01
## birth_cohort1800M1805  1.01
## birth_cohort1805M1810  1.00
## birth_cohort1810M1815  1.00
## birth_cohort1815M1820  1.01
## birth_cohort1820M1825  1.00
## birth_cohort1825M1830  1.00
## birth_cohort1830M1835  1.01
## male1                  1.00
## maternalage.factor1420 1.00
## maternalage.factor3550 1.00
## paternalage.mean       1.00
## paternal_loss01        1.00
## paternal_loss15        1.00
## paternal_loss510       1.00
## paternal_loss1015      1.00
## paternal_loss1520      1.00
## paternal_loss2025      1.00
## paternal_loss2530      1.00
## paternal_loss3035      1.00
## paternal_loss3540      1.00
## paternal_loss4045      1.00
## maternal_loss01        1.00
## maternal_loss15        1.00
## maternal_loss510       1.00
## maternal_loss1015      1.00
## maternal_loss1520      1.00
## maternal_loss2025      1.00
## maternal_loss2530      1.00
## maternal_loss3035      1.00
## maternal_loss3540      1.00
## maternal_loss4045      1.00
## older_siblings1        1.00
## older_siblings2        1.00
## older_siblings3        1.00
## older_siblings4        1.00
## older_siblings5P       1.00
## nr.siblings            1.00
## last_born1             1.00
## 
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
## is a crude measure of effective sample size, and Rhat is the potential 
## scale reduction factor on split chains (at convergence, Rhat = 1).

Table of fixed effects

fixed_eff = data.frame(model_summary$fixed, check.names = F)
fixed_eff$Est.Error = fixed_eff$Eff.Sample = fixed_eff$Rhat = NULL
fixed_eff$`Odds/hazard ratio` = exp(fixed_eff$Estimate)
fixed_eff$`OR/HR low 95%` = exp(fixed_eff$`l-95% CI`)
fixed_eff$`OR/HR high 95%` = exp(fixed_eff$`u-95% CI`)
fixed_eff = fixed_eff %>% select(`Odds/hazard ratio`, `OR/HR low 95%`, `OR/HR high 95%`)
pander::pander(fixed_eff)

	Odds/hazard ratio	OR/HR low 95%	OR/HR high 95%
Intercept	3.147	1.889	5.208
paternalage	0.7887	0.5591	1.1
birth_cohort1760M1765	1.067	0.7324	1.573
birth_cohort1765M1770	1.585	1.122	2.24
birth_cohort1770M1775	1.21	0.8723	1.685
birth_cohort1775M1780	1.721	1.22	2.469
birth_cohort1780M1785	1.674	1.179	2.434
birth_cohort1785M1790	1.85	1.3	2.697
birth_cohort1790M1795	1.577	1.129	2.205
birth_cohort1795M1800	1.938	1.405	2.681
birth_cohort1800M1805	2.177	1.583	3.072
birth_cohort1805M1810	2.088	1.517	2.95
birth_cohort1810M1815	2.005	1.476	2.81
birth_cohort1815M1820	2.497	1.848	3.426
birth_cohort1820M1825	2.3	1.721	3.098
birth_cohort1825M1830	2.293	1.711	3.103
birth_cohort1830M1835	2.399	1.782	3.276
male1	0.6046	0.5404	0.6771
maternalage.factor1420	1.458	0.7322	3.234
maternalage.factor3550	1.022	0.848	1.227
paternalage.mean	1.113	0.7841	1.591
paternal_loss01	0.7052	0.4542	1.139
paternal_loss15	0.601	0.4431	0.8183
paternal_loss510	0.7176	0.5458	0.9539
paternal_loss1015	0.8613	0.6573	1.142
paternal_loss1520	0.8427	0.6519	1.096
paternal_loss2025	0.7907	0.6195	1.013
paternal_loss2530	0.8553	0.6731	1.083
paternal_loss3035	1.001	0.7912	1.271
paternal_loss3540	0.8645	0.6832	1.086
paternal_loss4045	0.8672	0.6704	1.134
maternal_loss01	0.3019	0.1923	0.4669
maternal_loss15	0.6703	0.4988	0.9027
maternal_loss510	0.5968	0.4578	0.7785
maternal_loss1015	0.6398	0.4907	0.8373
maternal_loss1520	0.6961	0.5335	0.9172
maternal_loss2025	0.8559	0.6603	1.114
maternal_loss2530	0.8064	0.6358	1.025
maternal_loss3035	0.8639	0.692	1.091
maternal_loss3540	1.04	0.8433	1.284
maternal_loss4045	0.8301	0.666	1.042
older_siblings1	0.9936	0.8315	1.208
older_siblings2	1.143	0.898	1.454
older_siblings3	1.038	0.7775	1.408
older_siblings4	1.135	0.7748	1.676
older_siblings5P	1.342	0.8151	2.26
nr.siblings	0.9677	0.9229	1.016
last_born1	0.9431	0.8139	1.094

Paternal age effect

pander::pander(paternal_age_10y_effect(model))

effect	median_estimate	ci_95	ci_80
estimate father 25y	0.71	[0.63;0.76]	[0.66;0.75]
estimate father 35y	0.65	[0.54;0.74]	[0.58;0.71]
percentage change	-5.19	[-14.79;2.01]	[-11.08;-0.37]
OR/IRR	0.79	[0.56;1.1]	[0.63;0.98]

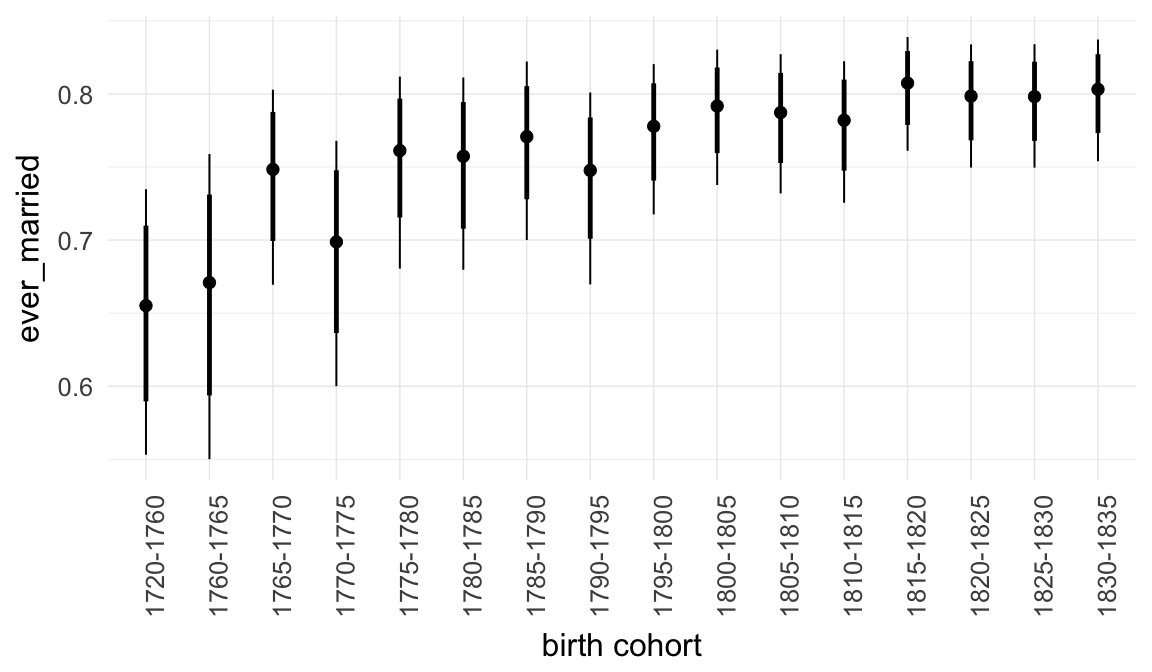
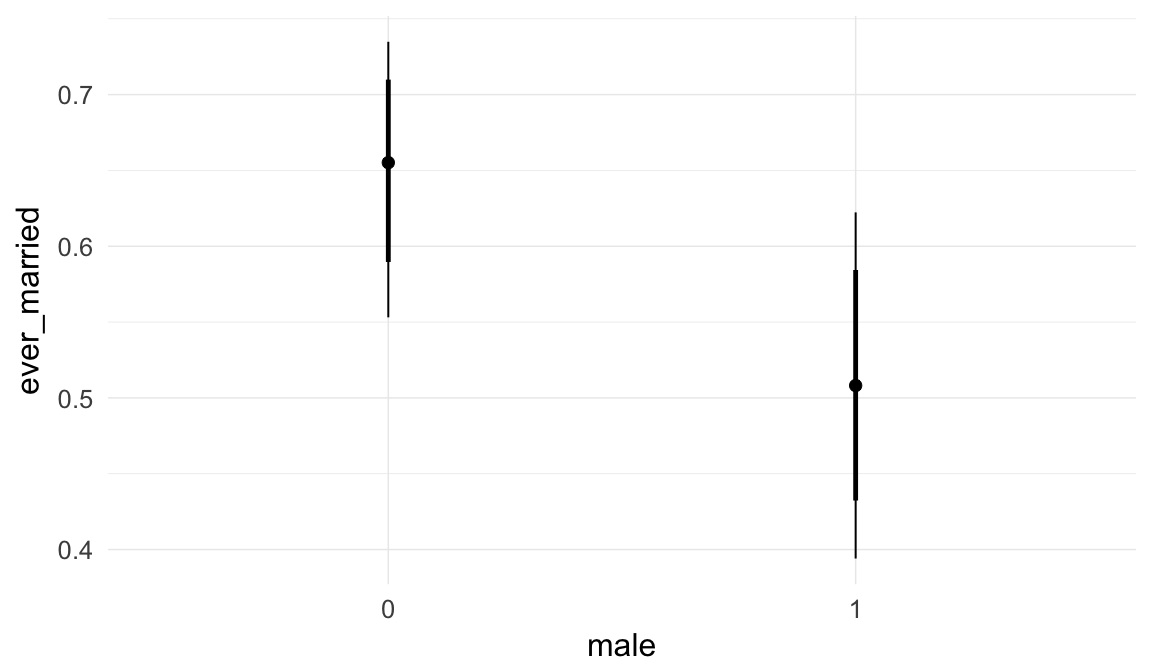
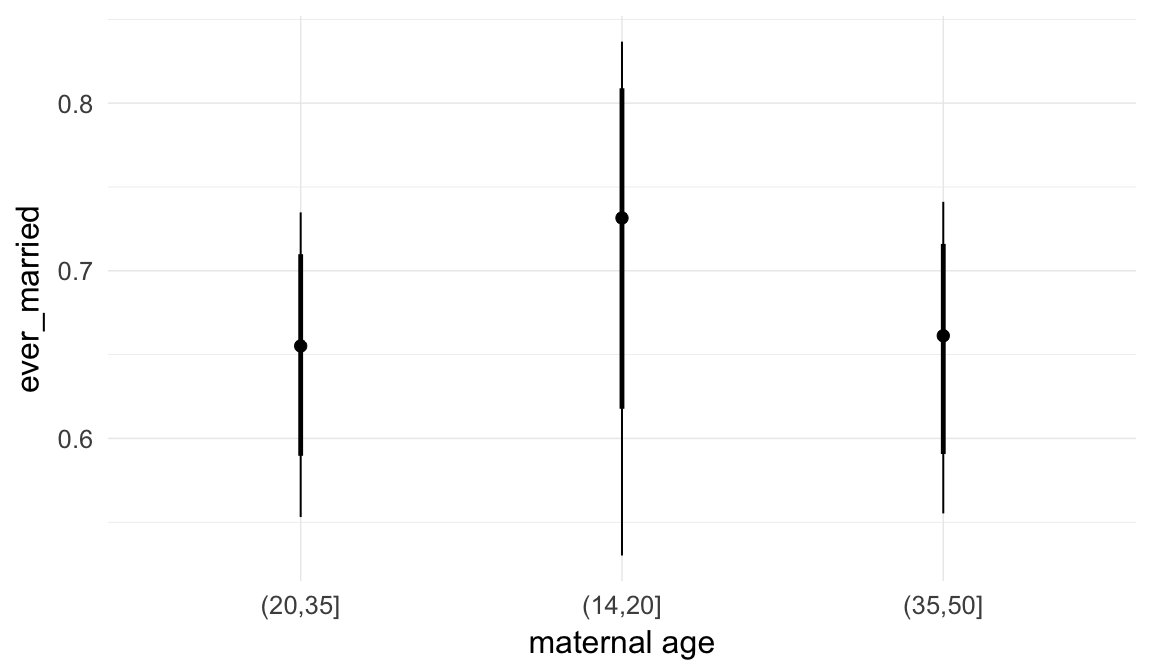
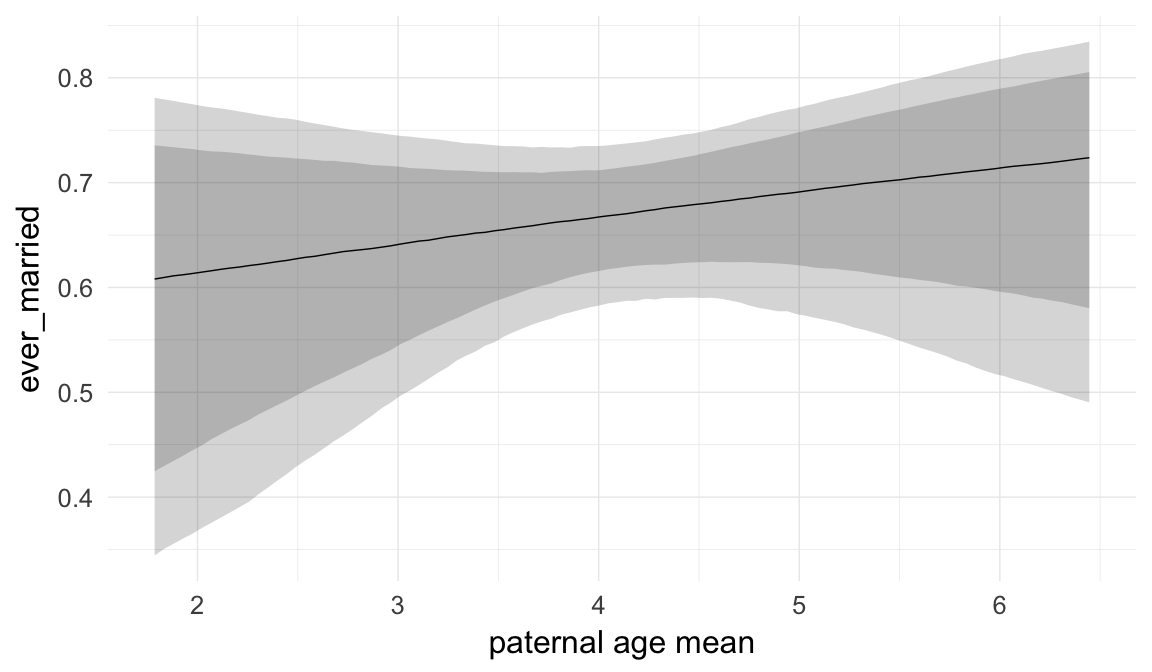
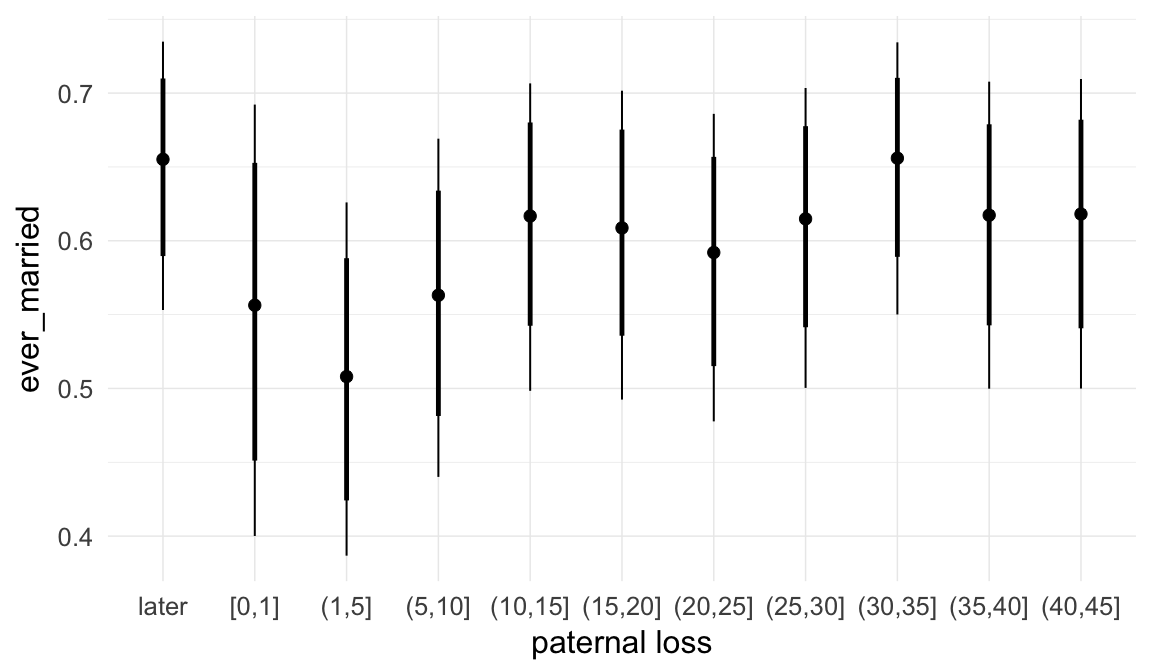
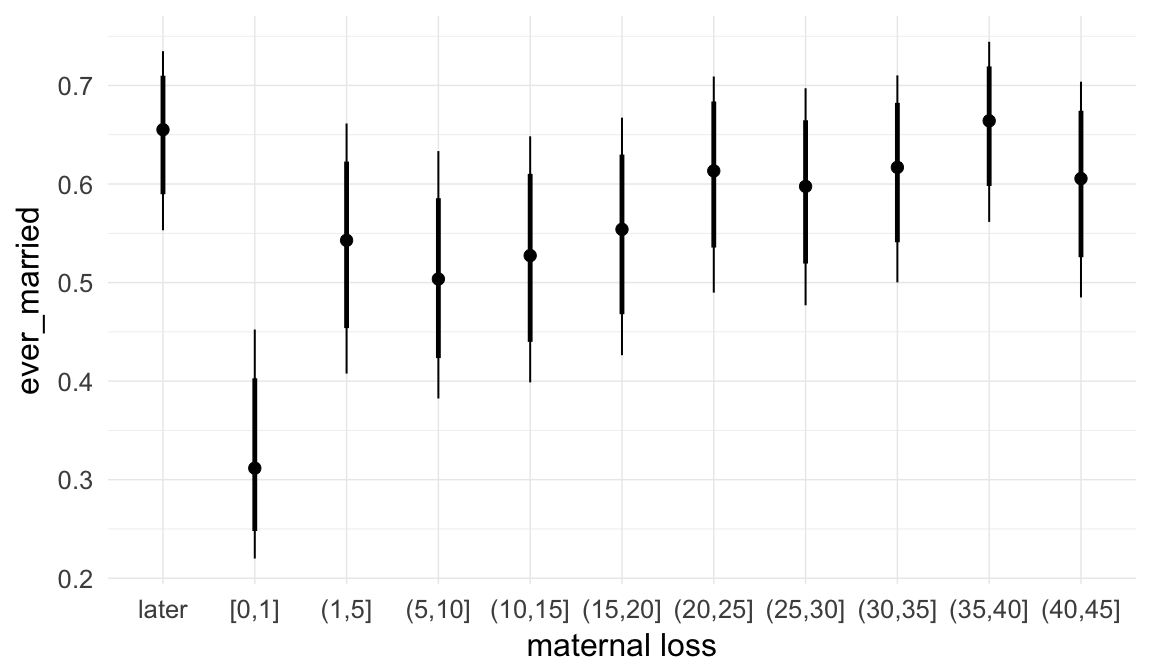
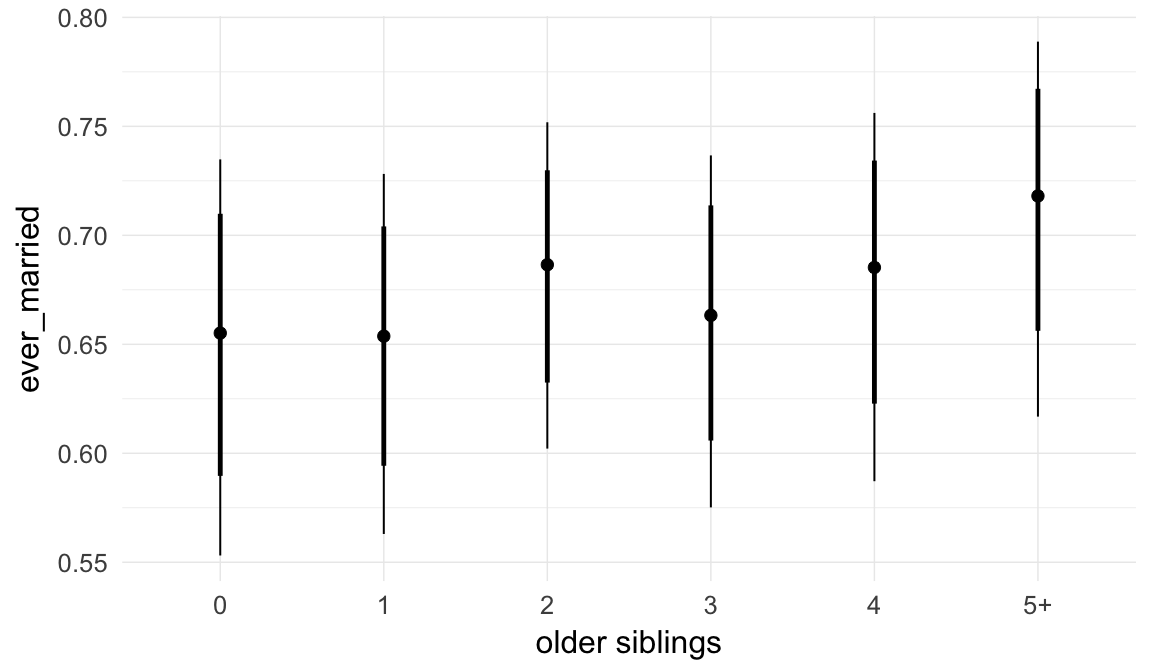
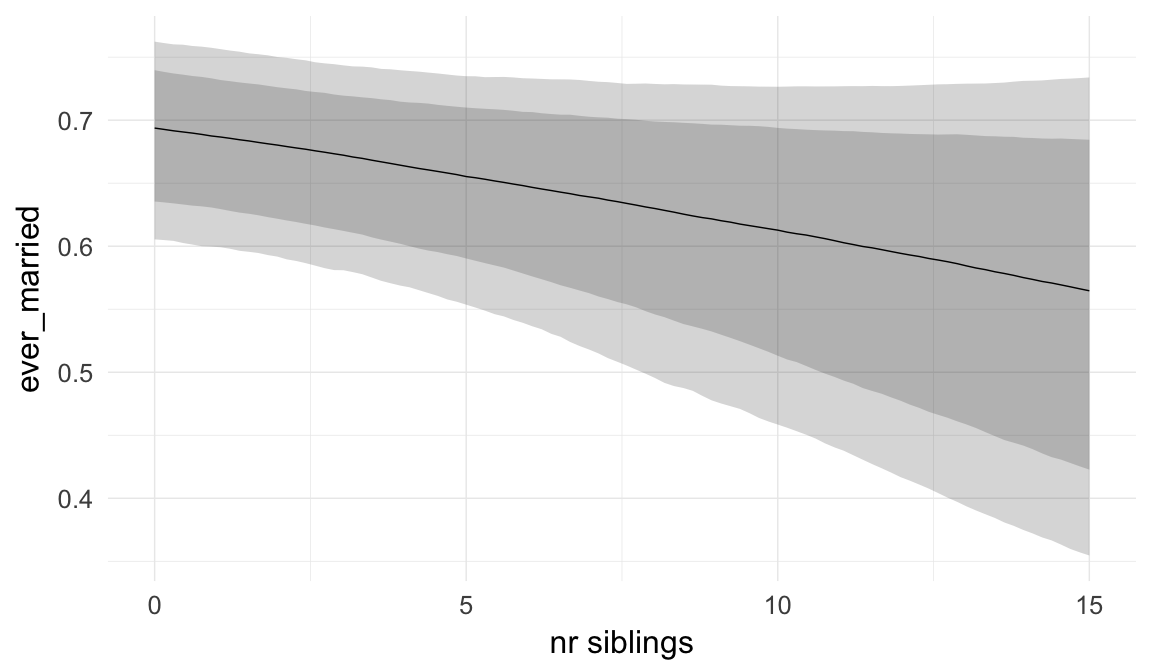
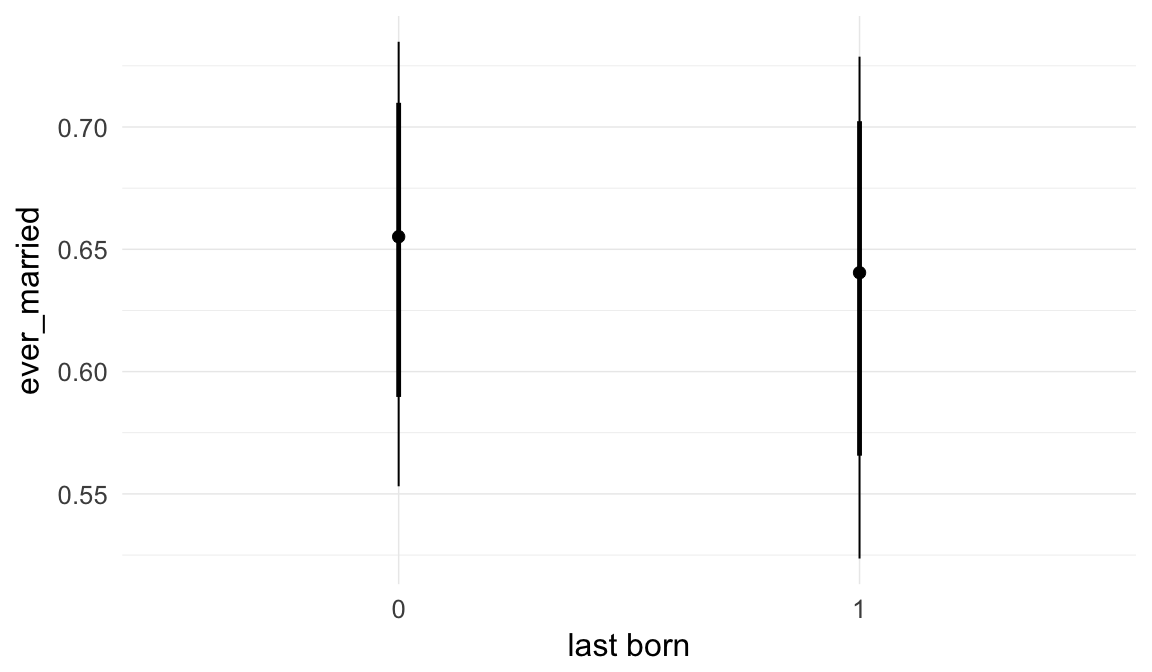
Marginal effect plots

plot.brmsMarginalEffects_shades(
    x = marginal_effects(model, re_formula = NA, probs = c(0.025,0.975)),
    y = marginal_effects(model, re_formula = NA, probs = c(0.1,0.9)), 
    ask = FALSE)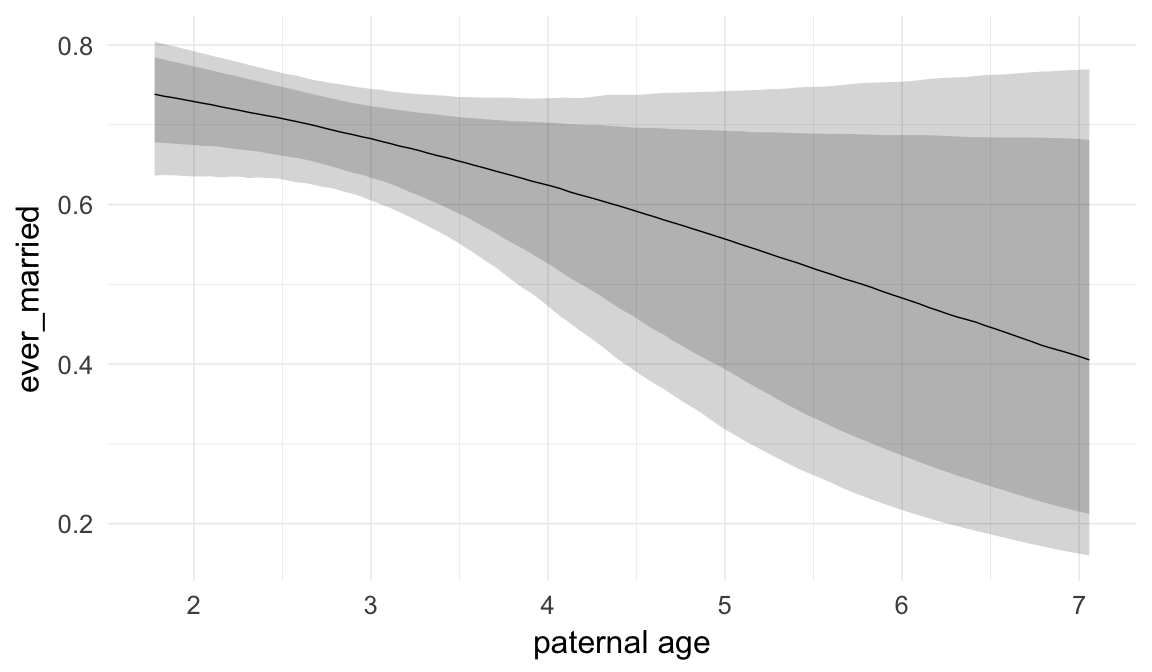

Coefficient plot

mcmc_areas(as.matrix(model$fit), regex_pars = "b_[^I]", point_est = "mean", prob = 0.50, prob_outer = 0.95) + ggtitle("Posterior densities with means and 50% intervals") + analysis_theme + theme(axis.text = element_text(size = 12), panel.grid = element_blank()) + xlab("Coefficient size")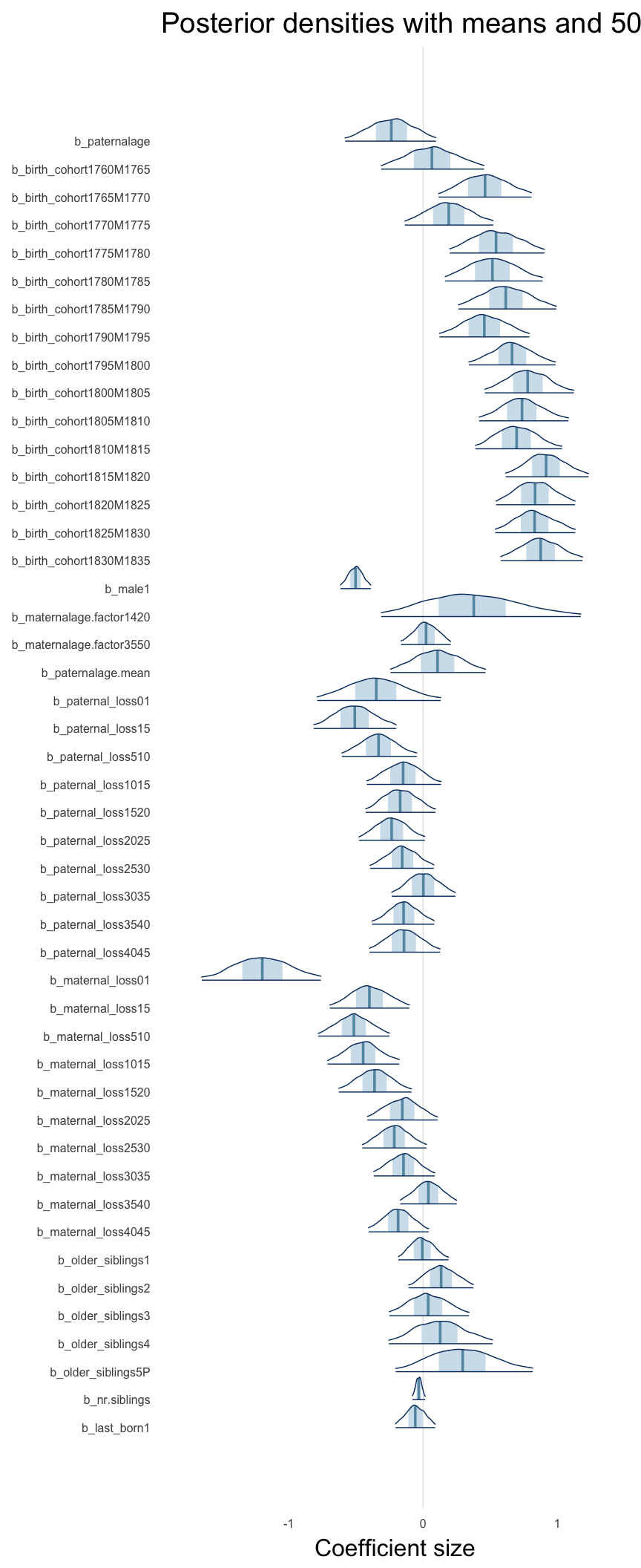

Diagnostics

These plots were made to diagnose misfit and nonconvergence.

Posterior predictive checks

In posterior predictive checks, we test whether we can approximately reproduce the real data distribution from our model.

brms::pp_check(model, re_formula = NA, type = "dens_overlay")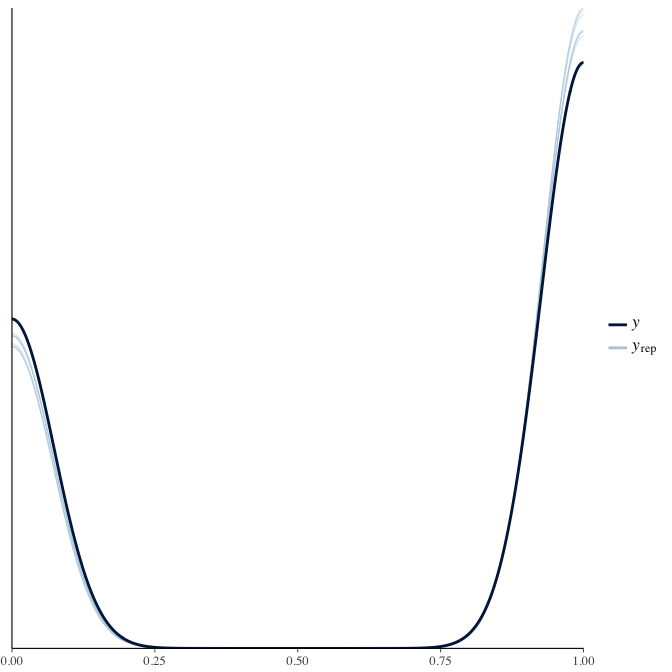

brms::pp_check(model, re_formula = NA, type = "hist")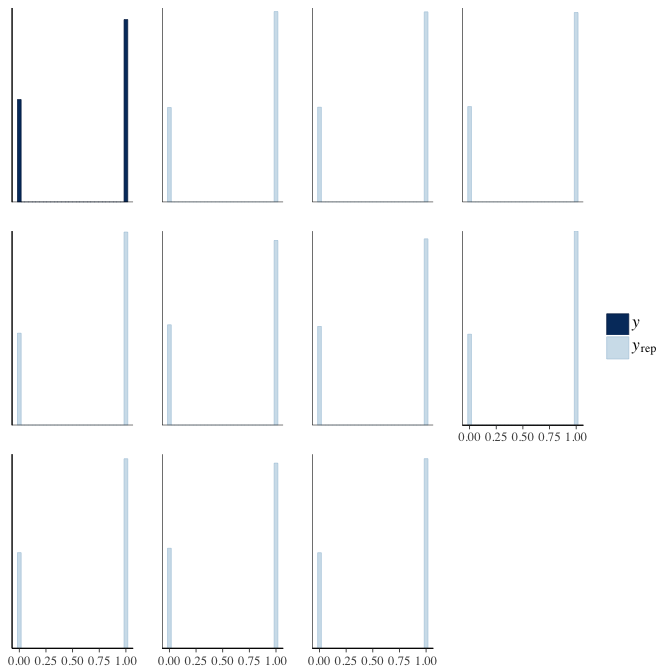

Rhat

Did the 6 chains converge?

stanplot(model, pars = "^b_[^I]", type = 'rhat')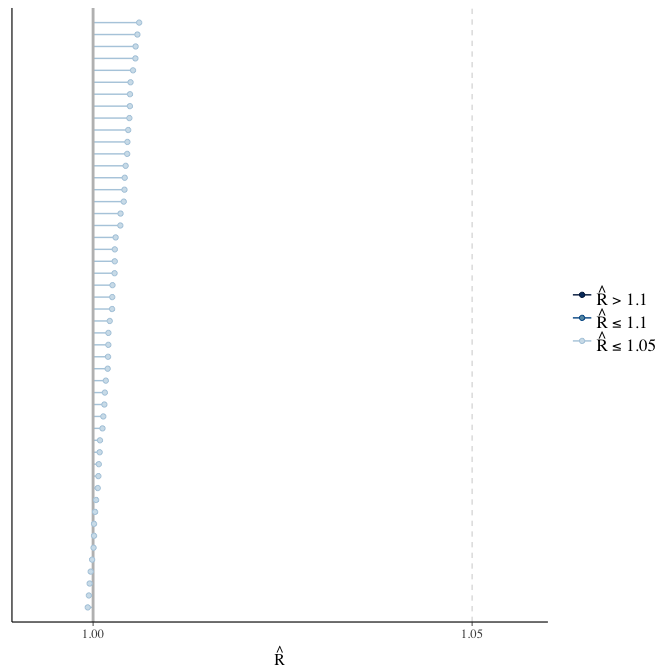

Effective sample size over average sample size

stanplot(model, pars = "^b", type = 'neff_hist')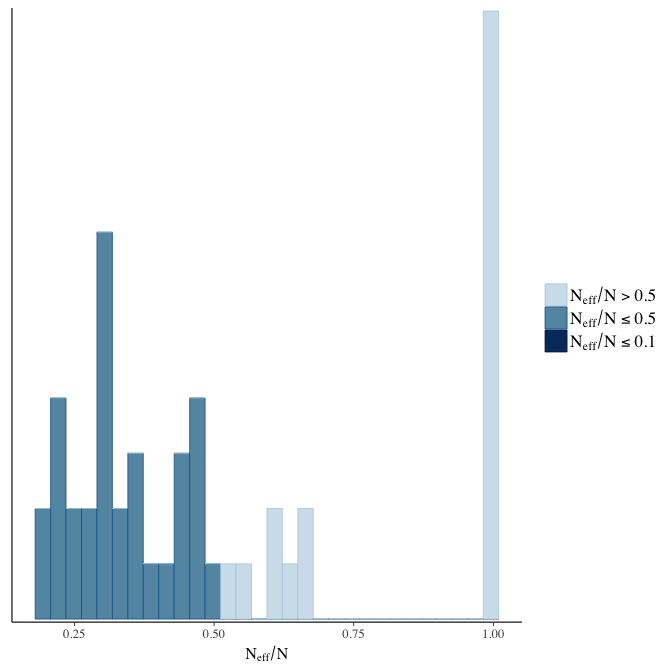

Trace plots

Trace plots are only shown in the case of nonconvergence.

if(any( summary(model)$fixed[,"Rhat"] > 1.1)) { # only do traceplots if not converged
    plot(model, N = 3, ask = FALSE)
}

File/cluster script name

This model was stored in the file: coefs/krmh/e3_ever_married.rds.

Click the following link to see the script used to generate this model:

opts_chunk$set(echo = FALSE)
clusterscript = str_replace(basename(model_filename), "\\.rds",".html")
cat("[Cluster script](" , clusterscript, ")", sep = "")

Cluster script

e4: Number of children

Here, we predict the number of children that the anchor had. To separate this effect from previous selective episodes, we include only ever-married anchors and control for their number of spouses (interacted with sex, because men tend to have more additional children from further spouses).

Model summary

Full summary

model_summary = summary(model, use_cache = FALSE, priors = TRUE)
print(model_summary)

##  Family: poisson(log) 
## Formula: children ~ paternalage + birth_cohort + spouses * male + maternalage.factor + paternalage.mean + paternal_loss + maternal_loss + older_siblings + nr.siblings + last_born + (1 | idParents) 
##    Data: model_data (Number of observations: 4431) 
## Samples: 6 chains, each with iter = 800; warmup = 300; thin = 1; 
##          total post-warmup samples = 3000
##    WAIC: Not computed
##  
## Priors: 
## b ~ normal(0,5)
## sd ~ student_t(3, 0, 5)
## 
## Group-Level Effects: 
## ~idParents (Number of levels: 1834) 
##               Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
## sd(Intercept)     0.38      0.01     0.35      0.4       1124    1
## 
## Population-Level Effects: 
##                        Estimate Est.Error l-95% CI u-95% CI Eff.Sample
## Intercept                  1.54      0.10     1.35     1.74       1209
## paternalage                0.15      0.06     0.04     0.26        954
## birth_cohort1760M1765     -0.02      0.07    -0.15     0.12       1495
## birth_cohort1765M1770     -0.05      0.06    -0.17     0.08       1040
## birth_cohort1770M1775     -0.14      0.07    -0.27    -0.01        950
## birth_cohort1775M1780      0.00      0.06    -0.13     0.12        826
## birth_cohort1780M1785     -0.02      0.06    -0.15     0.11        895
## birth_cohort1785M1790     -0.06      0.06    -0.18     0.07        840
## birth_cohort1790M1795     -0.04      0.06    -0.16     0.07        817
## birth_cohort1795M1800     -0.09      0.06    -0.20     0.03        733
## birth_cohort1800M1805     -0.08      0.06    -0.19     0.03        683
## birth_cohort1805M1810     -0.18      0.06    -0.29    -0.06        711
## birth_cohort1810M1815     -0.13      0.06    -0.24    -0.02        622
## birth_cohort1815M1820     -0.14      0.05    -0.25    -0.04        650
## birth_cohort1820M1825     -0.20      0.06    -0.31    -0.10        658
## birth_cohort1825M1830     -0.26      0.06    -0.36    -0.15        689
## birth_cohort1830M1835     -0.22      0.06    -0.33    -0.11        701
## spouses                    0.04      0.03    -0.02     0.10       2506
## male1                     -0.18      0.05    -0.28    -0.08       2127
## maternalage.factor1420    -0.09      0.09    -0.27     0.10       3000
## maternalage.factor3550    -0.04      0.03    -0.09     0.02       3000
## paternalage.mean          -0.17      0.06    -0.29    -0.06       1038
## paternal_loss01           -0.19      0.08    -0.35    -0.03       3000
## paternal_loss15           -0.05      0.06    -0.15     0.07       1663
## paternal_loss510          -0.03      0.05    -0.13     0.07       1342
## paternal_loss1015          0.04      0.05    -0.05     0.13       1365
## paternal_loss1520         -0.03      0.04    -0.11     0.06       1490
## paternal_loss2025         -0.07      0.04    -0.16     0.01       1330
## paternal_loss2530          0.01      0.04    -0.06     0.09       1437
## paternal_loss3035          0.01      0.04    -0.06     0.08       1491
## paternal_loss3540          0.03      0.03    -0.04     0.09       1802
## paternal_loss4045          0.01      0.04    -0.06     0.09       2165
## maternal_loss01           -0.02      0.09    -0.19     0.15       3000
## maternal_loss15           -0.11      0.05    -0.21    -0.01       1855
## maternal_loss510           0.04      0.05    -0.05     0.13       1673
## maternal_loss1015         -0.06      0.05    -0.16     0.03       1860
## maternal_loss1520          0.01      0.05    -0.08     0.10       1962
## maternal_loss2025         -0.04      0.04    -0.12     0.05       1877
## maternal_loss2530         -0.08      0.04    -0.15     0.00       1734
## maternal_loss3035         -0.13      0.04    -0.21    -0.06       1857
## maternal_loss3540         -0.07      0.03    -0.14    -0.01       1591
## maternal_loss4045         -0.09      0.03    -0.15    -0.02       3000
## older_siblings1            0.01      0.03    -0.05     0.06       1905
## older_siblings2           -0.08      0.04    -0.15     0.00       1196
## older_siblings3           -0.11      0.05    -0.20    -0.01       1023
## older_siblings4           -0.18      0.06    -0.30    -0.07       1003
## older_siblings5P          -0.20      0.08    -0.35    -0.04       1000
## nr.siblings                0.01      0.01    -0.01     0.03       1256
## last_born1                -0.05      0.02    -0.09     0.00       3000
## spouses:male1              0.24      0.04     0.16     0.33       2115
##                        Rhat
## Intercept              1.00
## paternalage            1.01
## birth_cohort1760M1765  1.00
## birth_cohort1765M1770  1.00
## birth_cohort1770M1775  1.00
## birth_cohort1775M1780  1.00
## birth_cohort1780M1785  1.00
## birth_cohort1785M1790  1.01
## birth_cohort1790M1795  1.01
## birth_cohort1795M1800  1.01
## birth_cohort1800M1805  1.01
## birth_cohort1805M1810  1.01
## birth_cohort1810M1815  1.01
## birth_cohort1815M1820  1.00
## birth_cohort1820M1825  1.01
## birth_cohort1825M1830  1.00
## birth_cohort1830M1835  1.00
## spouses                1.00
## male1                  1.00
## maternalage.factor1420 1.00
## maternalage.factor3550 1.00
## paternalage.mean       1.01
## paternal_loss01        1.00
## paternal_loss15        1.01
## paternal_loss510       1.00
## paternal_loss1015      1.01
## paternal_loss1520      1.01
## paternal_loss2025      1.00
## paternal_loss2530      1.00
## paternal_loss3035      1.00
## paternal_loss3540      1.00
## paternal_loss4045      1.00
## maternal_loss01        1.00
## maternal_loss15        1.00
## maternal_loss510       1.00
## maternal_loss1015      1.00
## maternal_loss1520      1.00
## maternal_loss2025      1.00
## maternal_loss2530      1.00
## maternal_loss3035      1.00
## maternal_loss3540      1.00
## maternal_loss4045      1.00
## older_siblings1        1.00
## older_siblings2        1.00
## older_siblings3        1.00
## older_siblings4        1.00
## older_siblings5P       1.00
## nr.siblings            1.00
## last_born1             1.00
## spouses:male1          1.00
## 
## Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample 
## is a crude measure of effective sample size, and Rhat is the potential 
## scale reduction factor on split chains (at convergence, Rhat = 1).

Table of fixed effects

fixed_eff = data.frame(model_summary$fixed, check.names = F)
fixed_eff$Est.Error = fixed_eff$Eff.Sample = fixed_eff$Rhat = NULL
fixed_eff$`Odds/hazard ratio` = exp(fixed_eff$Estimate)
fixed_eff$`OR/HR low 95%` = exp(fixed_eff$`l-95% CI`)
fixed_eff$`OR/HR high 95%` = exp(fixed_eff$`u-95% CI`)
fixed_eff = fixed_eff %>% select(`Odds/hazard ratio`, `OR/HR low 95%`, `OR/HR high 95%`)
pander::pander(fixed_eff)

	Odds/hazard ratio	OR/HR low 95%	OR/HR high 95%
Intercept	4.683	3.849	5.674
paternalage	1.157	1.039	1.293
birth_cohort1760M1765	0.9814	0.8588	1.127
birth_cohort1765M1770	0.9518	0.8398	1.082
birth_cohort1770M1775	0.8684	0.766	0.9894
birth_cohort1775M1780	0.9958	0.8749	1.128
birth_cohort1780M1785	0.9816	0.8634	1.116
birth_cohort1785M1790	0.9451	0.8357	1.069
birth_cohort1790M1795	0.9567	0.8503	1.076
birth_cohort1795M1800	0.9179	0.8181	1.029
birth_cohort1800M1805	0.9244	0.8283	1.032
birth_cohort1805M1810	0.835	0.7462	0.9374
birth_cohort1810M1815	0.8788	0.7875	0.9834
birth_cohort1815M1820	0.866	0.7804	0.9631
birth_cohort1820M1825	0.8148	0.7305	0.9086
birth_cohort1825M1830	0.7723	0.6946	0.8607
birth_cohort1830M1835	0.7988	0.717	0.8916
spouses	1.041	0.9775	1.11
male1	0.8342	0.7523	0.927
maternalage.factor1420	0.9171	0.7634	1.103
maternalage.factor3550	0.9639	0.9103	1.022
paternalage.mean	0.844	0.7506	0.9464
paternal_loss01	0.8287	0.708	0.9685
paternal_loss15	0.9558	0.8564	1.07
paternal_loss510	0.9681	0.8807	1.067
paternal_loss1015	1.037	0.9507	1.135
paternal_loss1520	0.9719	0.8945	1.057
paternal_loss2025	0.9286	0.8558	1.008
paternal_loss2530	1.011	0.9402	1.09
paternal_loss3035	1.01	0.9404	1.084
paternal_loss3540	1.027	0.9621	1.096
paternal_loss4045	1.013	0.9424	1.089
maternal_loss01	0.9838	0.8291	1.161
maternal_loss15	0.8975	0.8079	0.9937
maternal_loss510	1.041	0.9522	1.139
maternal_loss1015	0.9387	0.8556	1.028
maternal_loss1520	1.011	0.9231	1.107
maternal_loss2025	0.962	0.883	1.048
maternal_loss2530	0.923	0.8566	0.9955
maternal_loss3035	0.8747	0.8131	0.9393
maternal_loss3540	0.9281	0.8737	0.9861
maternal_loss4045	0.9173	0.8578	0.9783
older_siblings1	1.008	0.9523	1.064
older_siblings2	0.9273	0.8629	0.9965
older_siblings3	0.9002	0.8165	0.9921
older_siblings4	0.8327	0.7395	0.9367
older_siblings5P	0.822	0.7041	0.9625
nr.siblings	1.011	0.9946	1.027
last_born1	0.9527	0.9104	0.9983
spouses:male1	1.273	1.168	1.386

Paternal age effect

pander::pander(paternal_age_10y_effect(model))

effect	median_estimate	ci_95	ci_80
estimate father 25y	4.15	[3.71;4.64]	[3.86;4.46]
estimate father 35y	4.8	[4.19;5.53]	[4.38;5.27]
percentage change	15.62	[3.92;29.31]	[7.67;24.68]
OR/IRR	1.16	[1.04;1.29]	[1.08;1.25]

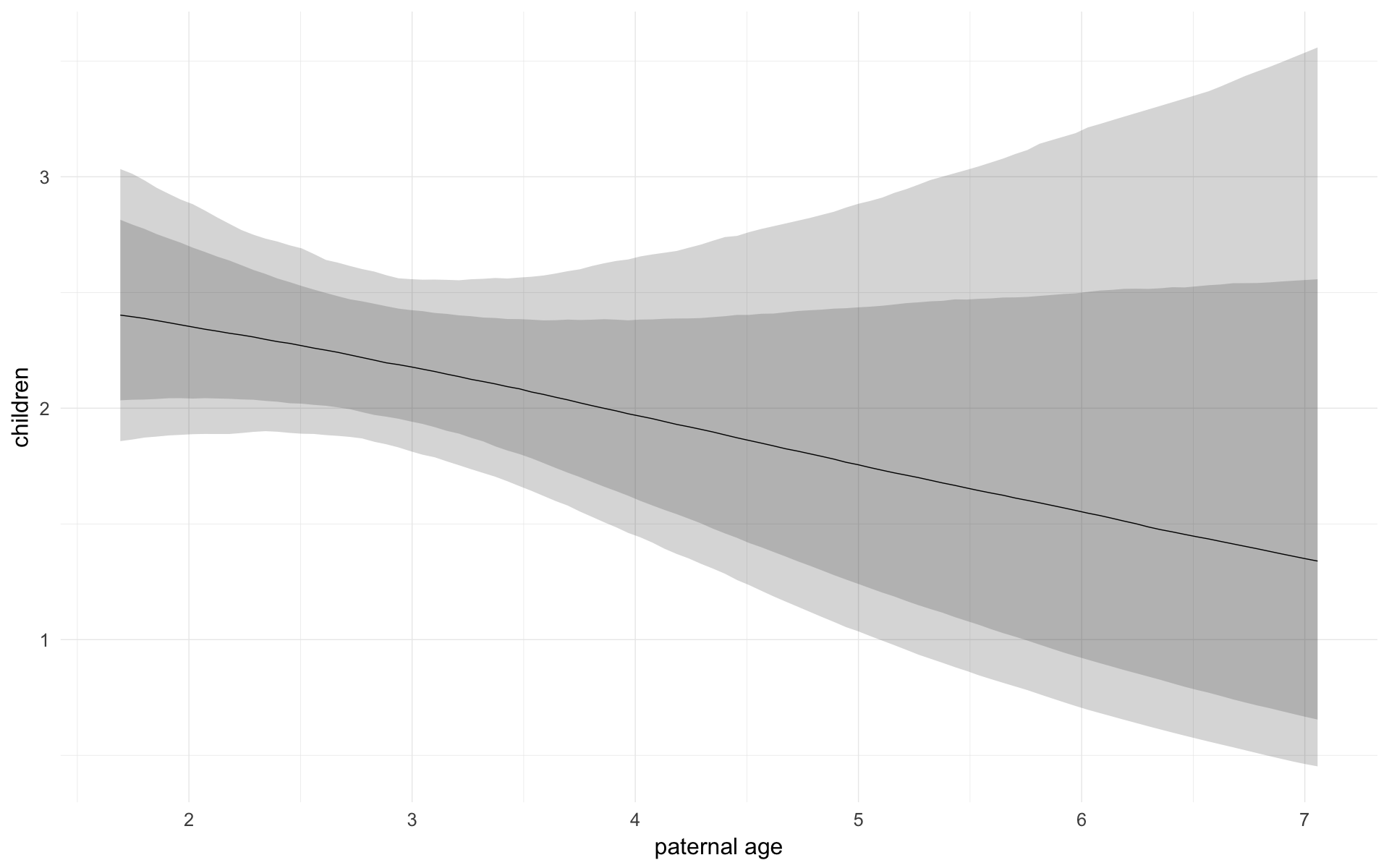
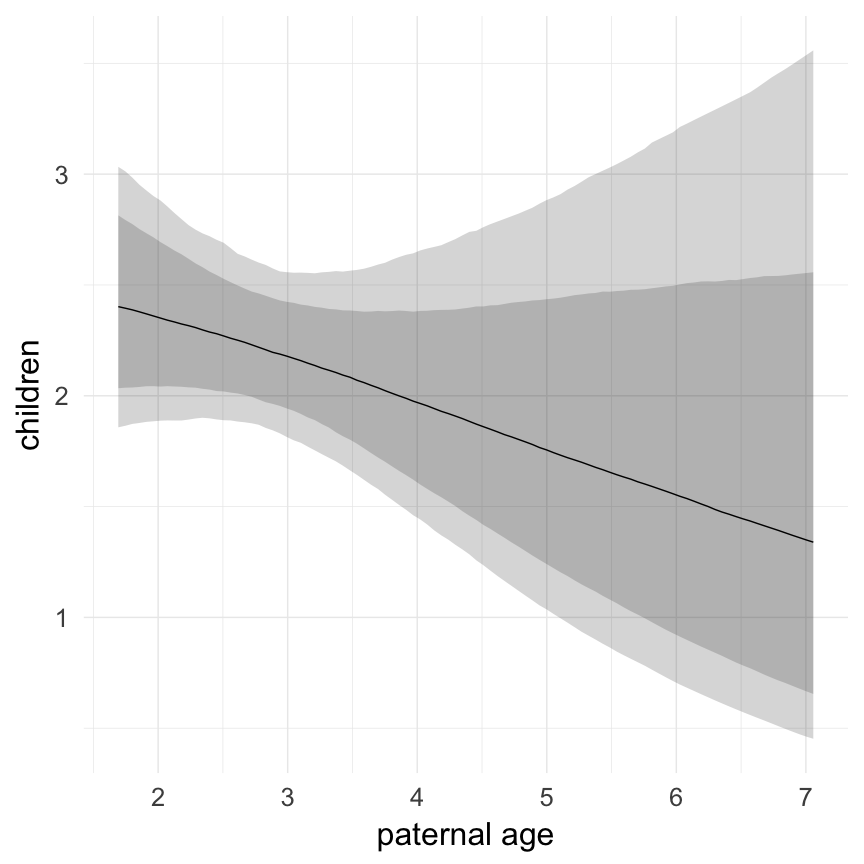
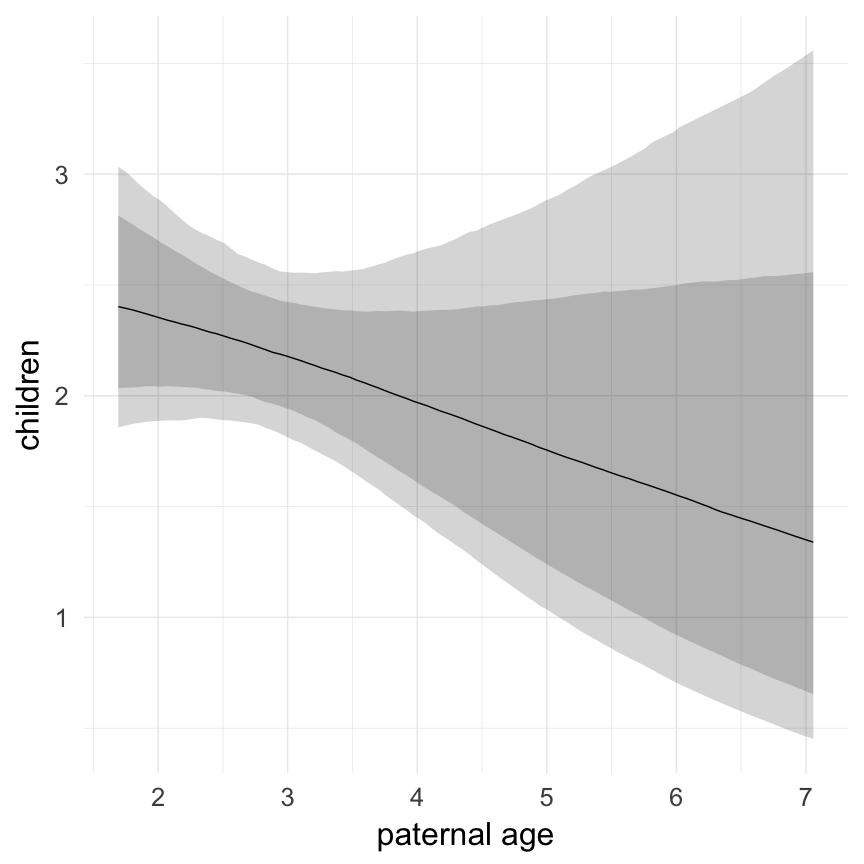
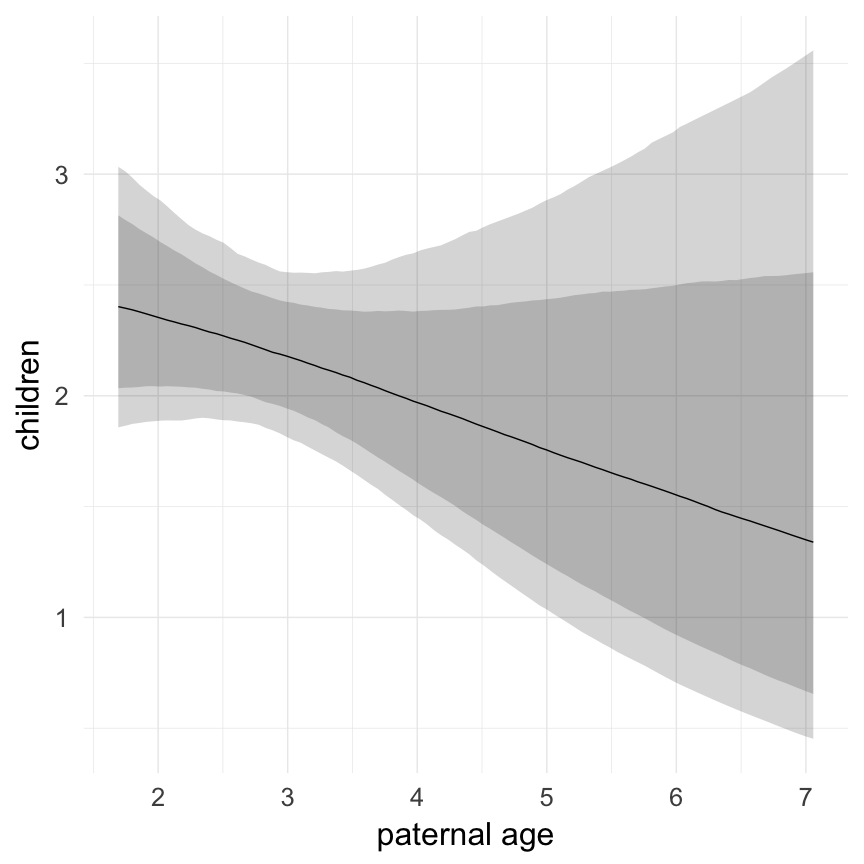
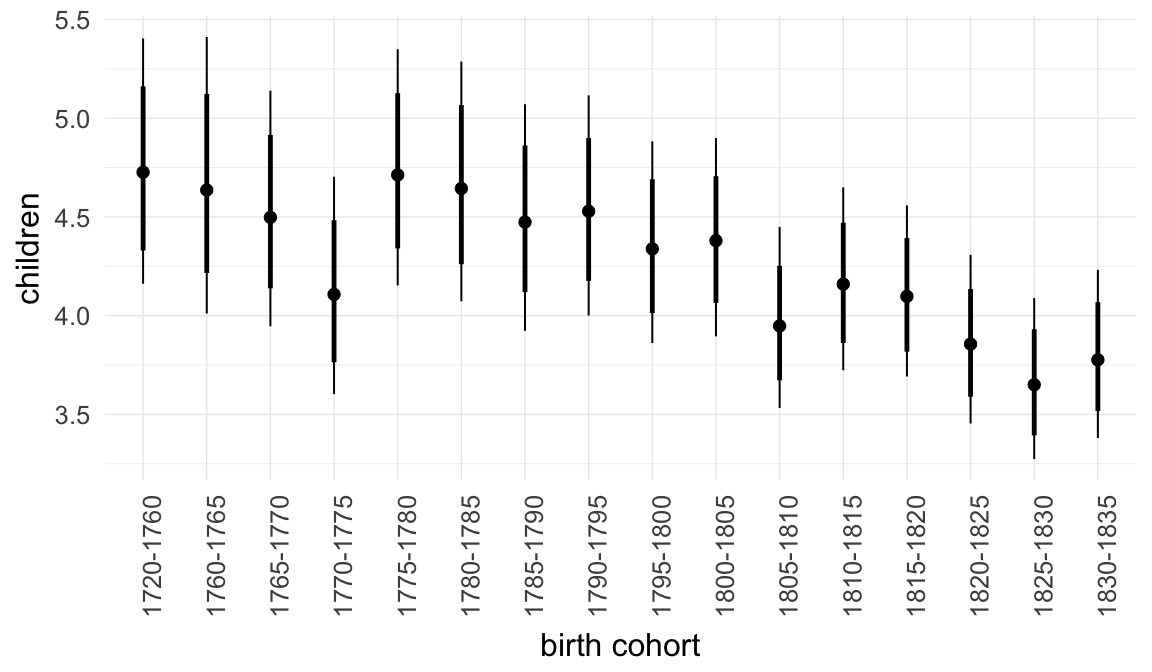
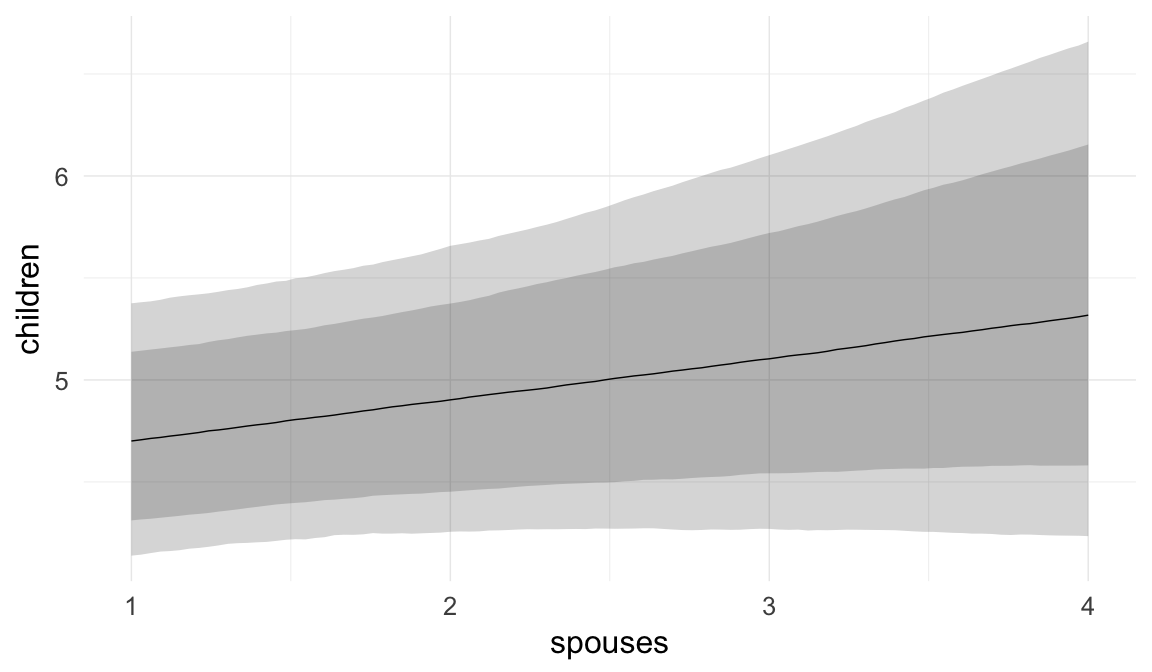
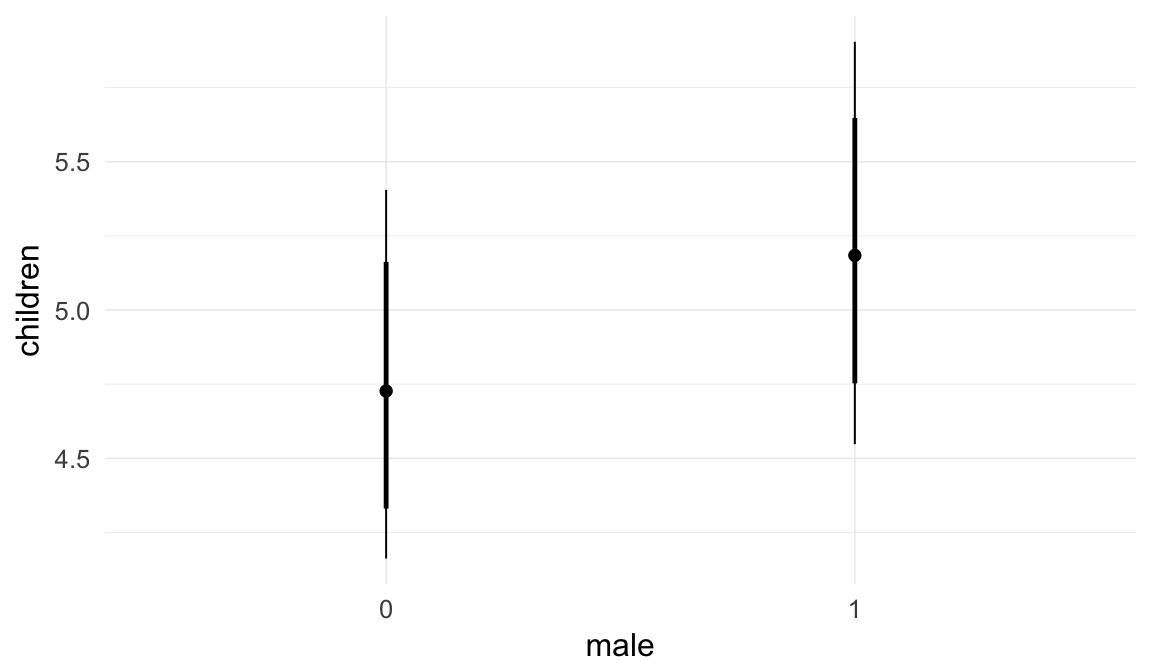
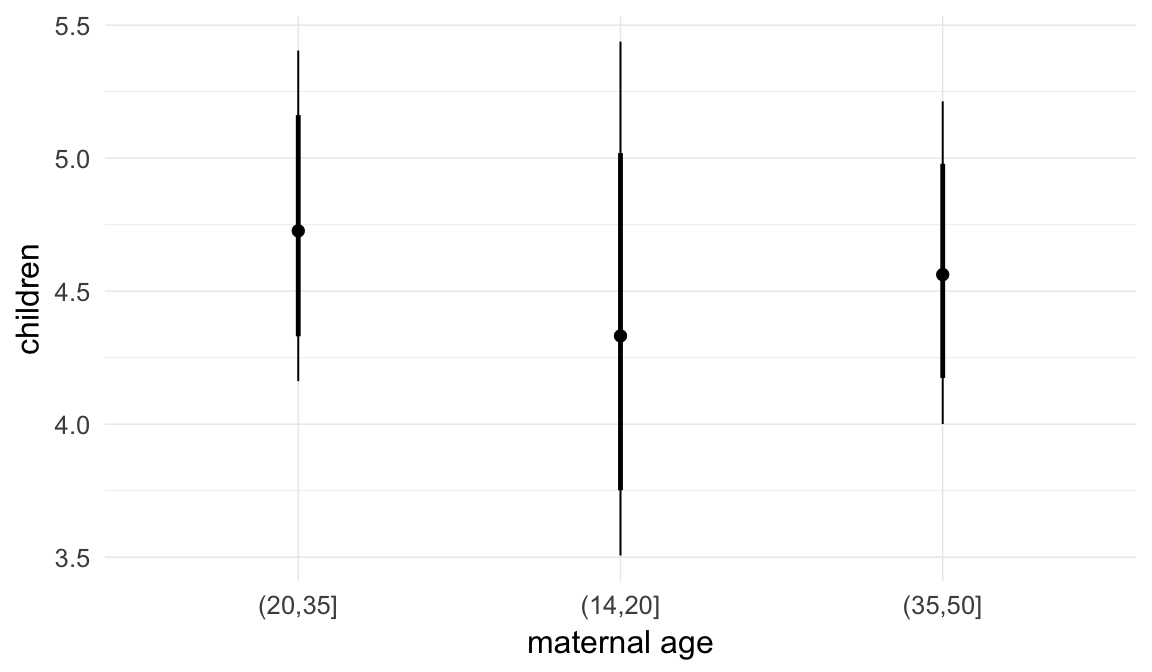
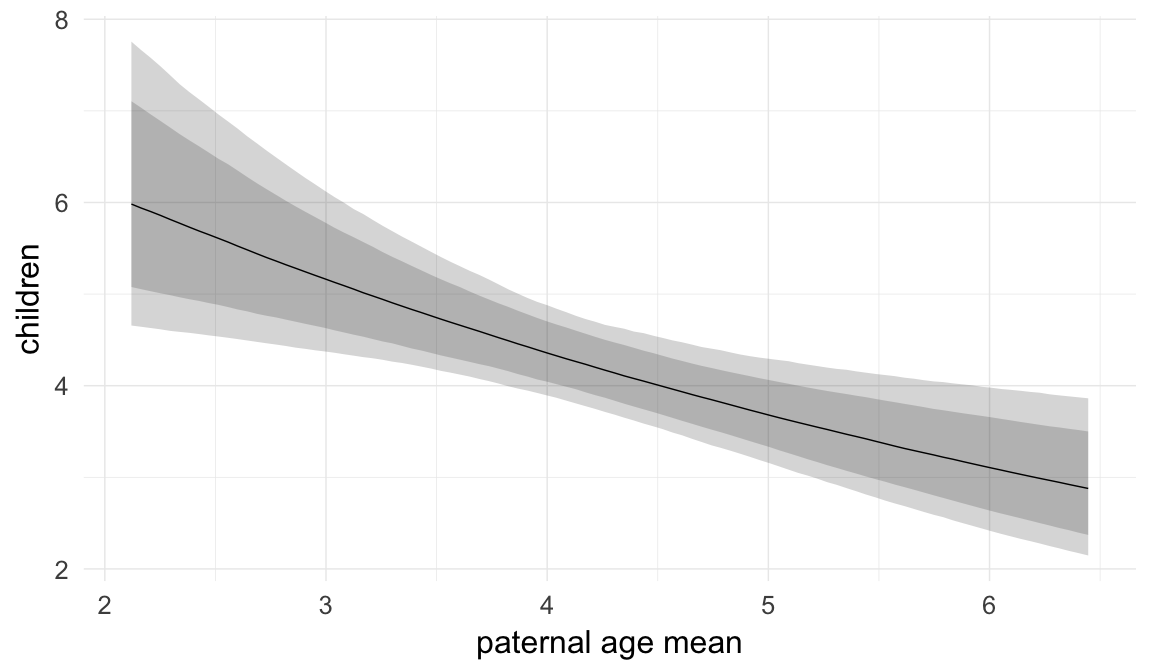
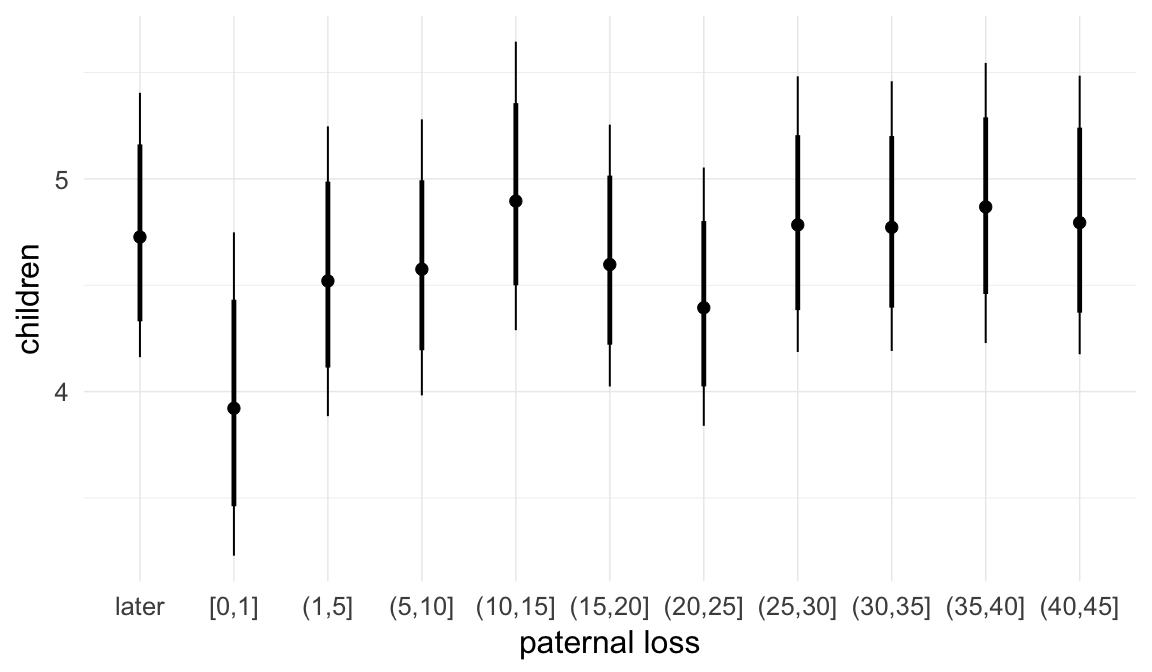
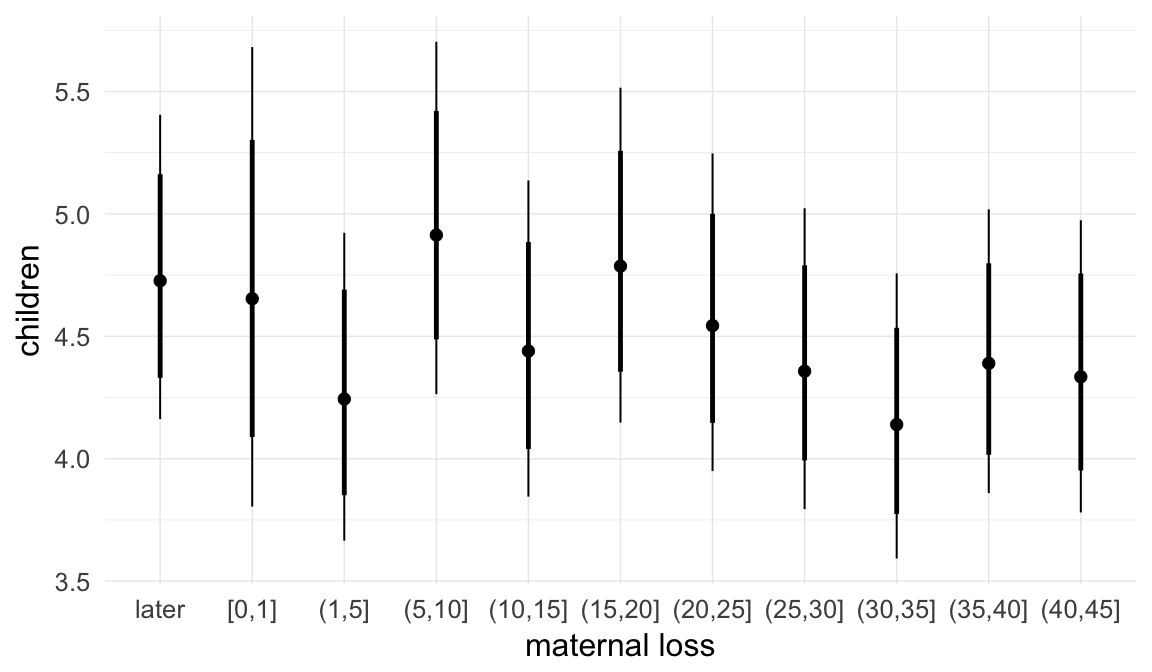
Marginal effect plots

plot.brmsMarginalEffects_shades(
    x = marginal_effects(model, re_formula = NA, probs = c(0.025,0.975)),
    y = marginal_effects(model, re_formula = NA, probs = c(0.1,0.9)), 
    ask = FALSE)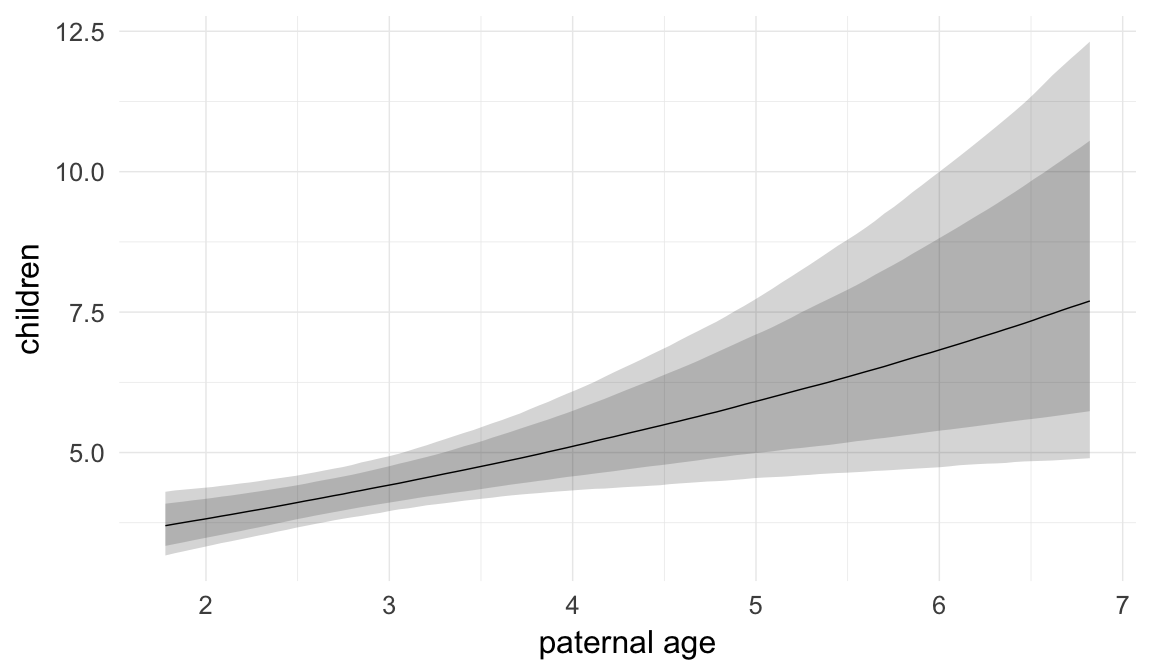

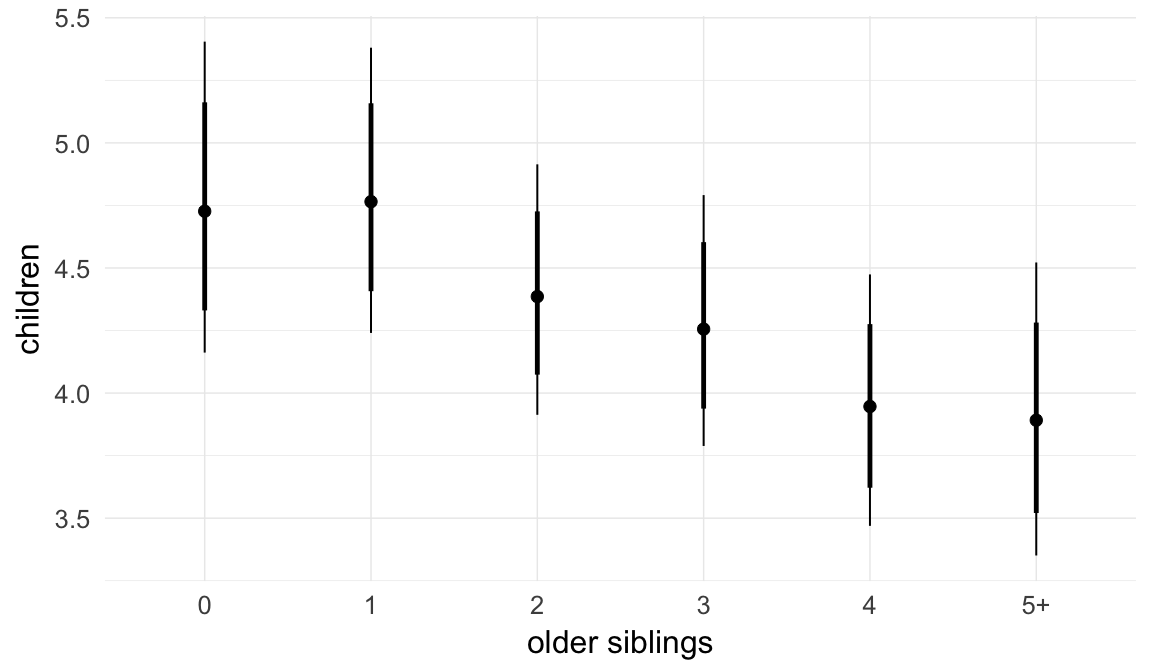
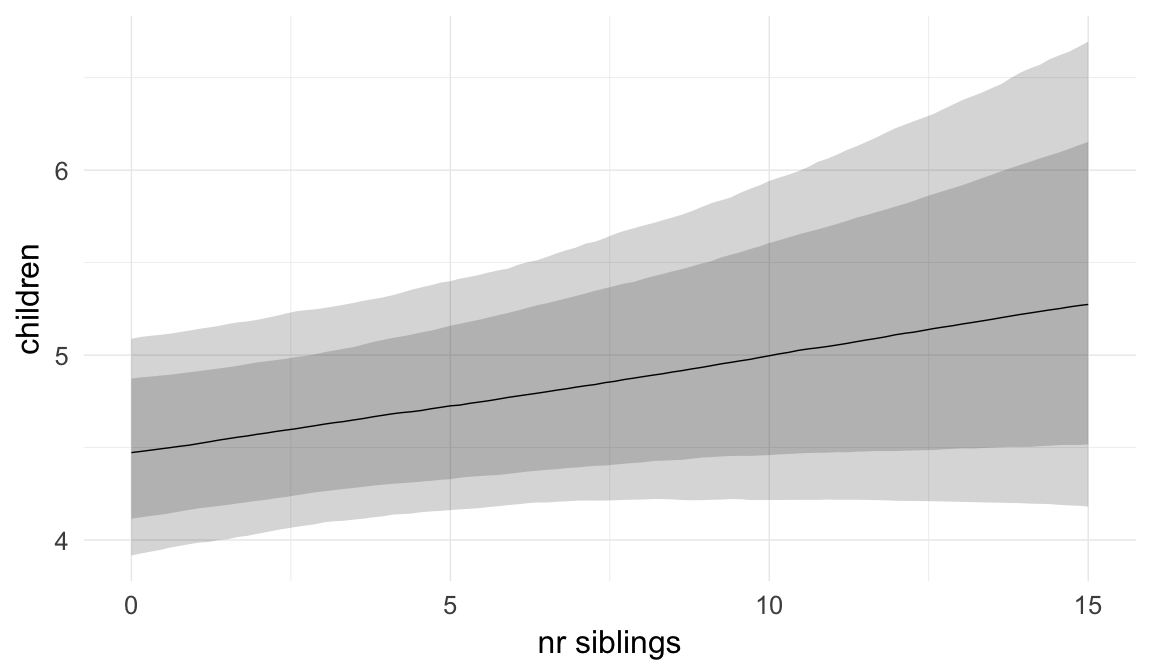
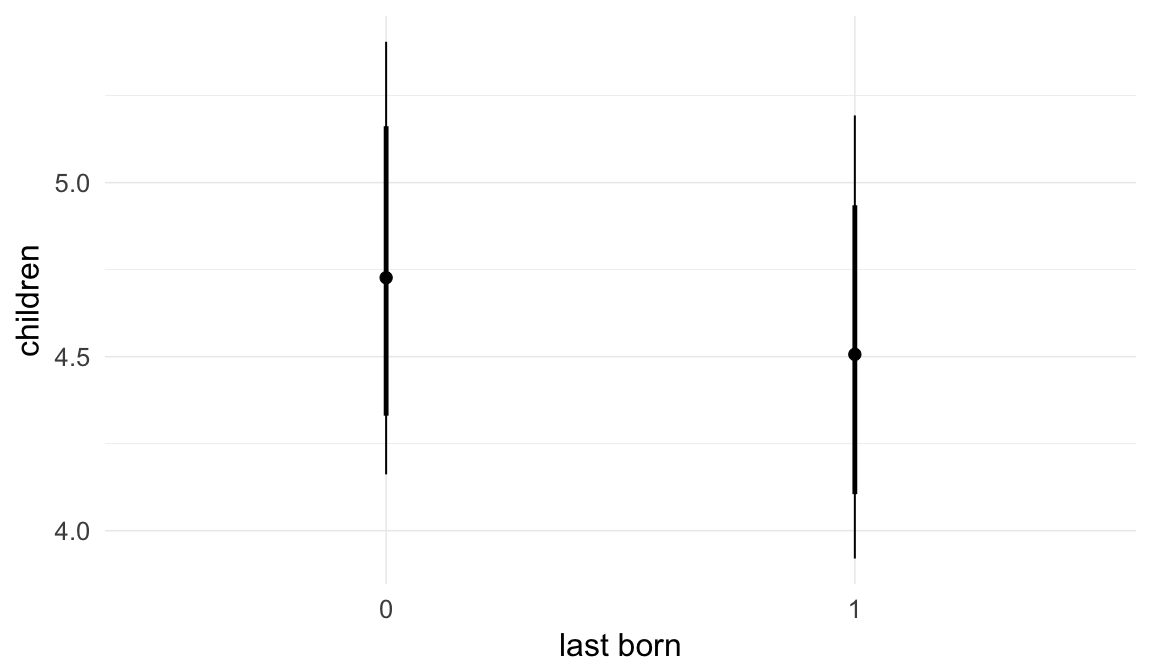
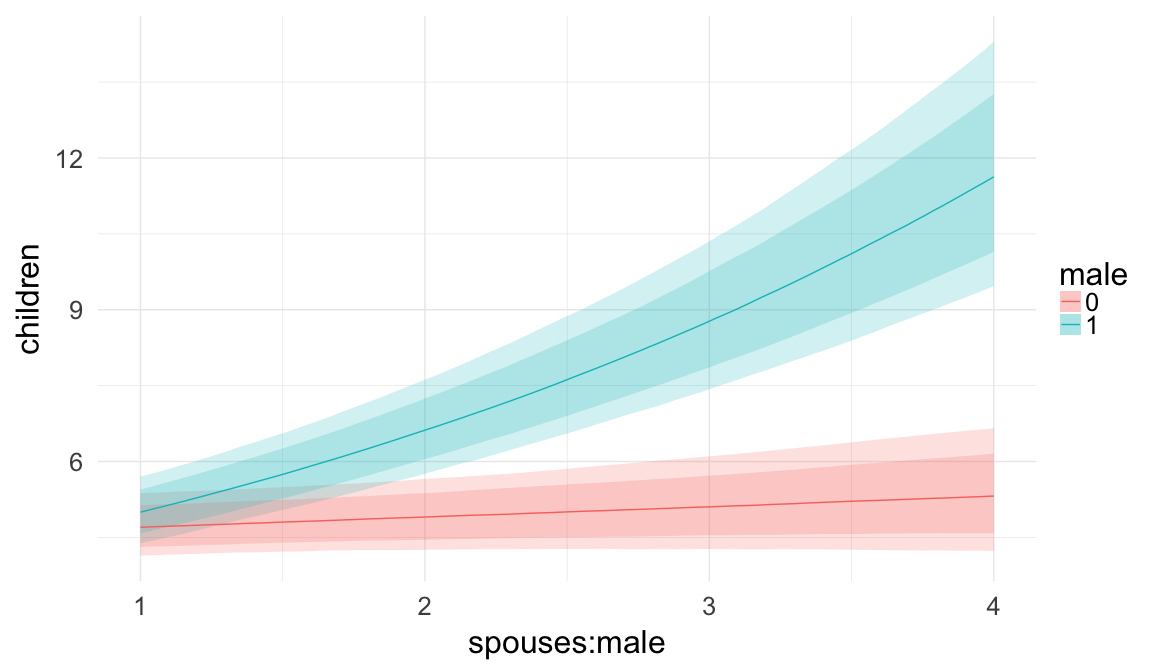
Coefficient plot

mcmc_areas(as.matrix(model$fit), regex_pars = "b_[^I]", point_est = "mean", prob = 0.50, prob_outer = 0.95) + ggtitle("Posterior densities with means and 50% intervals") + analysis_theme + theme(axis.text = element_text(size = 12), panel.grid = element_blank()) + xlab("Coefficient size")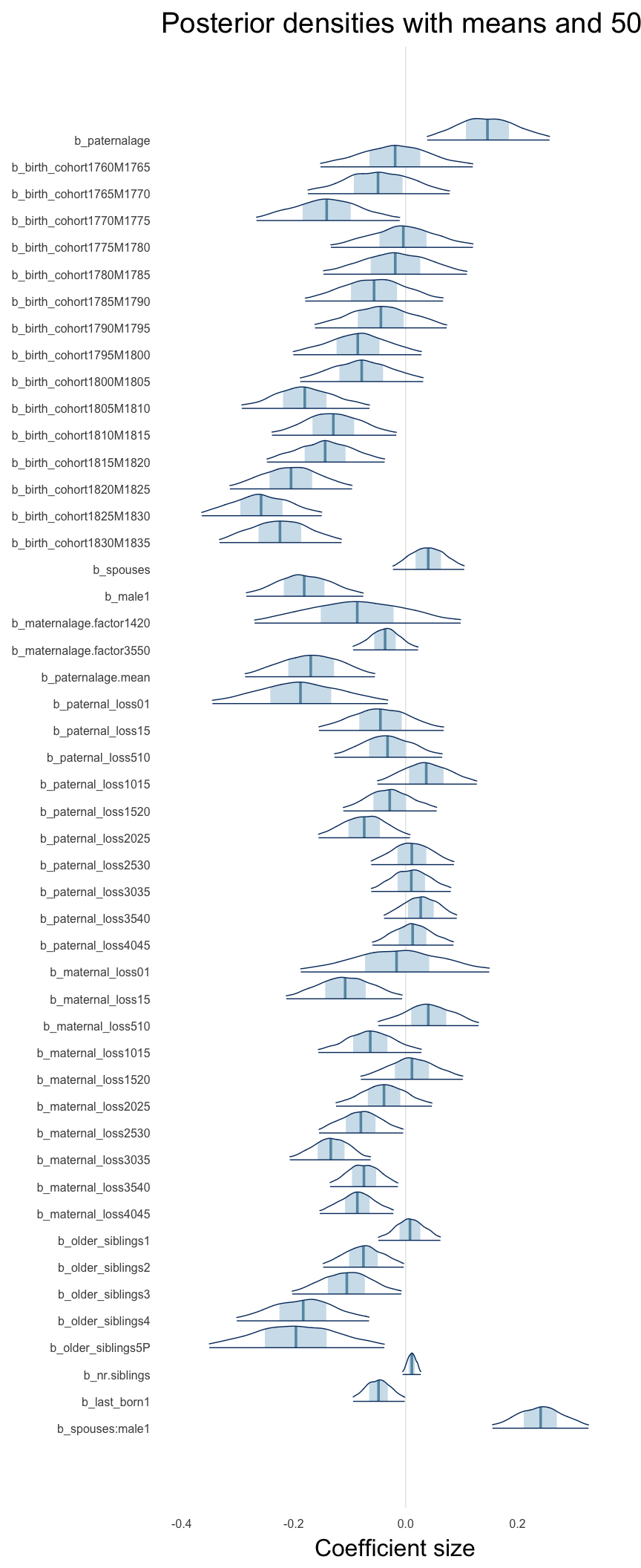

Diagnostics

These plots were made to diagnose misfit and nonconvergence.

Posterior predictive checks

In posterior predictive checks, we test whether we can approximately reproduce the real data distribution from our model.

brms::pp_check(model, re_formula = NA, type = "dens_overlay")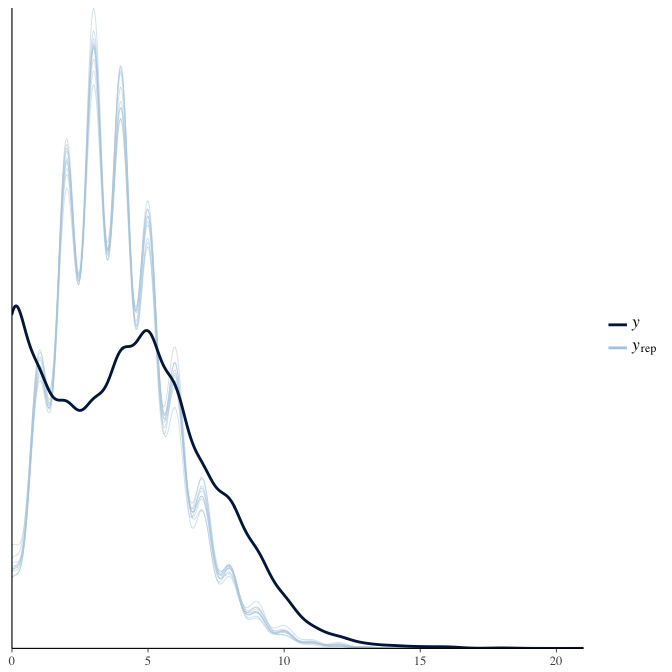

brms::pp_check(model, re_formula = NA, type = "hist")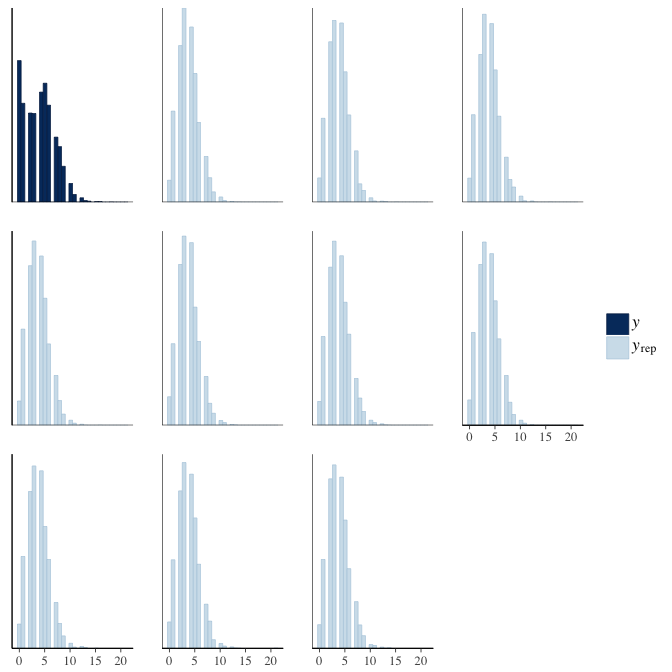

Rhat

Did the 6 chains converge?

stanplot(model, pars = "^b_[^I]", type = 'rhat')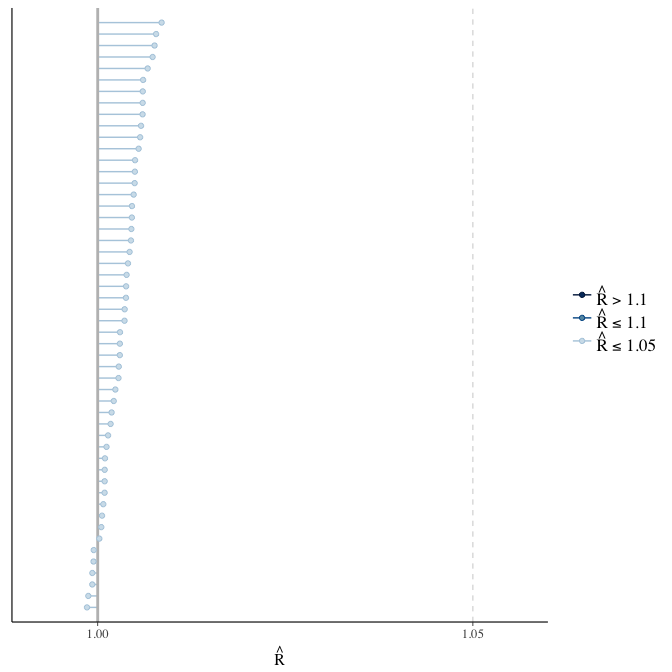

Effective sample size over average sample size

stanplot(model, pars = "^b", type = 'neff_hist')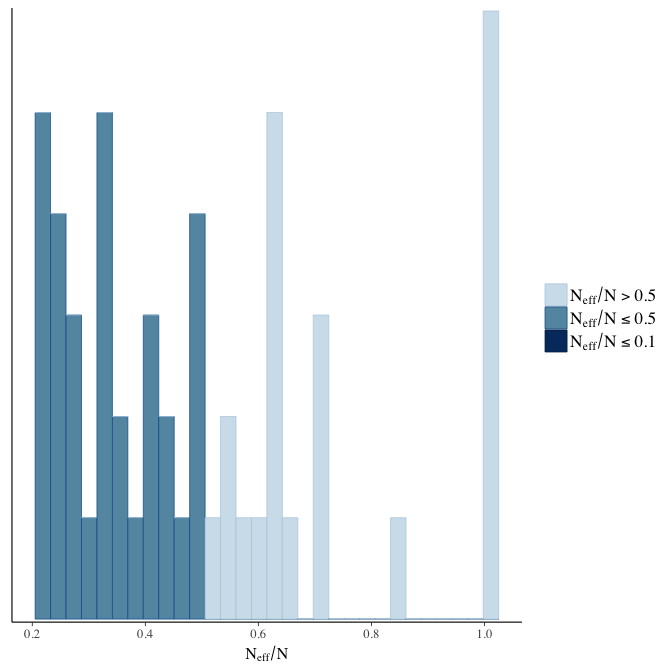

Trace plots

Trace plots are only shown in the case of nonconvergence.

if(any( summary(model)$fixed[,"Rhat"] > 1.1)) { # only do traceplots if not converged
    plot(model, N = 3, ask = FALSE)
}

File/cluster script name

This model was stored in the file: coefs/krmh/e4_children.rds.

Click the following link to see the script used to generate this model:

opts_chunk$set(echo = FALSE)
clusterscript = str_replace(basename(model_filename), "\\.rds",".html")
cat("[Cluster script](" , clusterscript, ")", sep = "")

Cluster script

e5: Probability of ever divorcing

Here, we predict the probability of ever divorcing. To separate this effect from previous selective episodes, we include only ever-married anchors. Divorce data was only analysed in modern Sweden.

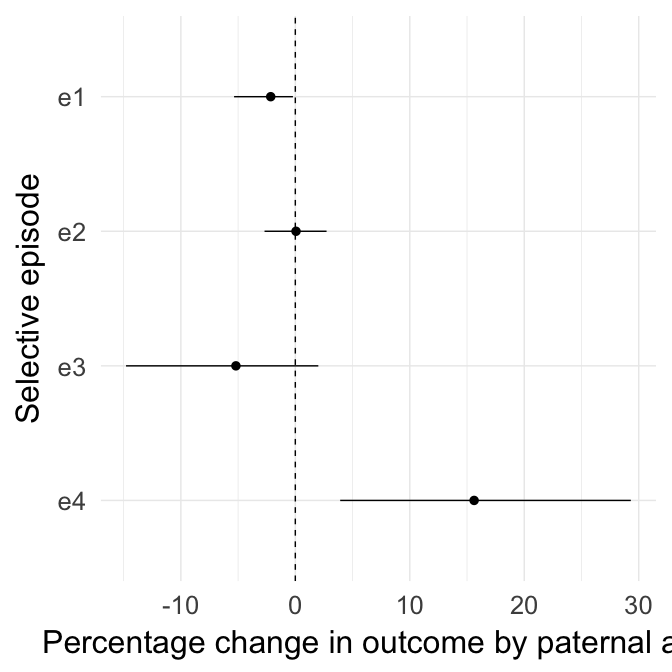
All episodes

Here we show the effect of paternal age for each episode.